| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 13 Surface Areas And Volumes
Welcome to the solutions guide for Chapter 13: Surface Areas And Volumes. This chapter significantly elevates our study of three-dimensional geometry, moving beyond the analysis of individual, standard solids like the cube, cuboid, cylinder, cone, sphere, and hemisphere. Here, we tackle more intricate scenarios involving the calculation of surface areas and volumes for objects constructed by combinations of these basic solid shapes. Imagine toys constructed from cones and hemispheres, medicinal capsules formed by cylinders capped with hemispheres, or tents combining cylindrical bases with conical tops – these composite structures require careful consideration of how surfaces join and volumes aggregate. Furthermore, this chapter explores the dynamic process of transforming solids from one shape into another, such as when metal is melted and recast, introducing the fundamental principle of volume conservation. Additionally, for syllabi that include it, we delve into a specific derived shape: the frustum of a cone, the shape resembling a bucket or a lampshade, which results from slicing off the top portion of a cone with a plane parallel to its base. Successfully navigating this chapter demands strong spatial visualization skills, precise application of surface area and volume formulas, and adept algebraic manipulation.
A primary focus is calculating the surface area and volume of combinations of solids. The solutions emphasize distinct strategies for each calculation:
- Surface Area: When calculating the total surface area of a combined solid, the key is to identify and sum only the areas of the surfaces that are exposed or visible externally. Importantly, the areas where the constituent solids are joined together are not included in the total surface area. For instance, the surface area of a tent composed of a cylinder topped by a cone would be the sum of the Curved Surface Area (CSA) of the cylinder and the CSA of the cone (assuming the base is open or on the ground).
- Volume: Calculating the volume of a combined solid is generally more straightforward. It simply involves summing the individual volumes of the basic shapes that make up the composite object. For example, the volume of a toy shaped like a cone mounted on a hemisphere is the sum of the volume of the cone and the volume of the hemisphere.
Examples explored include toys, architectural structures like pillars with hemispherical domes, industrial objects like tanks, and medical items like capsules.
The chapter also addresses problems involving the conversion of solids. This typically involves scenarios where a solid of one shape (e.g., a large metallic sphere) is melted down and recast into one or more solids of another shape (e.g., smaller spheres, a cylindrical wire, or numerous small cubes). The unwavering physical principle governing these transformations is that of Volume Conservation: the volume of the material remains constant throughout the process. Therefore, the core strategy is to equate the volume of the original solid to the total volume of the solid(s) formed after recasting ($\text{Volume}_{\text{original}} = \text{Volume}_{\text{final}}$). Solutions demonstrate using this principle to find unknown dimensions (like the radius of a new sphere or the length of a wire) or to determine the number of smaller objects that can be created.
Lastly, the concept of the Frustum of a Cone is introduced (note: this may be excluded in rationalised syllabi). A frustum is the portion of a cone remaining when its top part is cut off by a plane parallel to the base. Let $\mathbf{r_1}$ and $\mathbf{r_2}$ be the radii of the larger and smaller circular ends, respectively, $\mathbf{h}$ be the perpendicular height, and $\mathbf{l}$ be the slant height. The solutions provide and apply the specific formulas for the frustum:
- Slant Height: $\mathbf{l} = \sqrt{\mathbf{h}^2 + (\mathbf{r_1} - \mathbf{r_2})^2}$
- Curved Surface Area (CSA): $CSA = \pi(\mathbf{r_1} + \mathbf{r_2})\mathbf{l}$
- Total Surface Area (TSA): $TSA = \pi(\mathbf{r_1} + \mathbf{r_2})\mathbf{l} + \pi \mathbf{r_1}^2 + \pi \mathbf{r_2}^2$
- Volume: $V = \frac{1}{3}\pi \mathbf{h}(\mathbf{r_1}^2 + \mathbf{r_2}^2 + \mathbf{r_1}\mathbf{r_2})$
Applications involve calculating the capacity (volume) and surface area of objects commonly shaped like frustums, such as buckets, drinking glasses, or lampshades. Mastery of this chapter hinges on careful interpretation of problems, accurate visualization, correct formula selection, and precise calculations.
Example 1 to 4 (Before Exercise 13.1)
Example 1. Rasheed got a playing top (lattu) as his birthday present, which surprisingly had no colour on it. He wanted to colour it with his crayons. The top is shaped like a cone surmounted by a hemisphere (see Fig 13.6). The entire top is 5 cm in height and the diameter of the top is 3.5 cm. Find the area he has to colour. (Take π = $\frac{22}{7}$ )
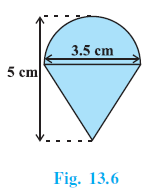
Answer:
Given:
The playing top is shaped like a cone surmounted by a hemisphere.
Total height of the top = 5 cm.
Diameter of the top = 3.5 cm.
Value of $\pi = \frac{22}{7}$.
To Find:
The total surface area of the top that needs to be coloured.
Solution:
The total surface area (TSA) of the top to be coloured is the sum of the curved surface area (CSA) of the hemisphere and the curved surface area (CSA) of the cone.
Diameter of the top = 3.5 cm.
Radius of the hemisphere (and base of the cone), $r = \frac{\text{Diameter}}{2} = \frac{3.5}{2} = 1.75$ cm.
Height of the hemispherical part = Radius = $r = 1.75$ cm.
Height of the conical part, $h = \text{Total height} - \text{Height of hemisphere}$
$h = 5 - 1.75 = 3.25$ cm.
Now, we need to find the slant height ($l$) of the cone.
The formula for slant height is $l = \sqrt{r^2 + h^2}$.
$l = \sqrt{(1.75)^2 + (3.25)^2}$
$l = \sqrt{3.0625 + 10.5625}$
$l = \sqrt{13.625}$
$l \approx 3.69$ cm. We can approximate this to $l \approx 3.7$ cm (as commonly done in textbook examples for this value).
Calculate the CSA of the hemisphere.
CSA of hemisphere = $2 \pi r^2$
CSA of hemisphere = $2 \times \frac{22}{7} \times (1.75)^2$
CSA of hemisphere = $2 \times \frac{22}{7} \times 1.75 \times 1.75$
CSA of hemisphere = $2 \times \frac{22}{\cancel{7}_1} \times \frac{175}{100} \times \frac{175}{100}$
CSA of hemisphere = $2 \times \frac{22}{1} \times \frac{25}{100} \times \frac{175}{100}$
CSA of hemisphere = $2 \times 22 \times \frac{1}{4} \times 1.75$
CSA of hemisphere = $11 \times 1.75 = 19.25$ cm$^2$.
Calculate the CSA of the cone.
CSA of cone = $\pi r l$
CSA of cone = $\frac{22}{7} \times 1.75 \times 3.7$ (using the approximate value of $l$)
CSA of cone = $\frac{22}{\cancel{7}_1} \times \frac{175^{\;25}}{100} \times 3.7$
CSA of cone = $\frac{22}{1} \times \frac{25}{100} \times 3.7$
CSA of cone = $22 \times \frac{1}{4} \times 3.7$
CSA of cone = $5.5 \times 3.7 = 20.35$ cm$^2$.
Total Surface Area of the top = CSA of hemisphere + CSA of cone
TSA = $19.25 + 20.35$
TSA = $39.6$ cm$^2$.
Hence, the area Rasheed has to colour is 39.6 cm$^2$.
Example 2. The decorative block shown in Fig. 13.7 is made of two solids — a cube and a hemisphere. The base of the block is a cube with edge 5 cm, and the hemisphere fixed on the top has a diameter of 4.2 cm. Find the total surface area of the block. (Take π = $\frac{22}{7}$ )
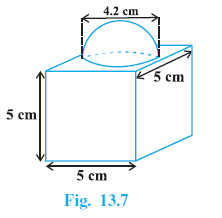
Answer:
Given:
A decorative block made of a cube and a hemisphere.
Edge length of the cube, $s = 5$ cm.
Diameter of the hemisphere fixed on top = 4.2 cm.
Value of $\pi = \frac{22}{7}$.
To Find:
The total surface area (TSA) of the block.
Solution:
The total surface area of the block consists of:
1. The total surface area of the cube.
2. The curved surface area (CSA) of the hemisphere.
3. We need to subtract the area of the base of the hemisphere because it covers a part of the top face of the cube.
TSA of block = (TSA of cube) - (Base area of hemisphere) + (CSA of hemisphere)
Calculate the TSA of the cube:
TSA of cube = $6 \times (\text{edge})^2 = 6s^2$
TSA of cube = $6 \times (5)^2 = 6 \times 25 = 150$ cm$^2$.
Calculate the dimensions and areas related to the hemisphere:
Diameter of hemisphere = 4.2 cm.
Radius of hemisphere, $r = \frac{\text{Diameter}}{2} = \frac{4.2}{2} = 2.1$ cm.
Base area of hemisphere = $\pi r^2$
Base area = $\frac{22}{7} \times (2.1)^2 = \frac{22}{7} \times 2.1 \times 2.1$
Base area = $22 \times 0.3 \times 2.1 = 6.6 \times 2.1 = 13.86$ cm$^2$.
Curved Surface Area (CSA) of hemisphere = $2 \pi r^2$
CSA of hemisphere = $2 \times (\text{Base area}) = 2 \times 13.86 = 27.72$ cm$^2$.
Calculate the total surface area of the block:
TSA of block = (TSA of cube) - (Base area of hemisphere) + (CSA of hemisphere)
TSA of block = $150 - 13.86 + 27.72$
TSA of block = $150 + (27.72 - 13.86)$
TSA of block = $150 + 13.86$
TSA of block = $163.86$ cm$^2$.
Alternatively, using the simplified formula TSA = $6s^2 + \pi r^2$:
TSA = $150 + 13.86 = 163.86$ cm$^2$.
Hence, the total surface area of the block is 163.86 cm$^2$.
Example 3. A wooden toy rocket is in the shape of a cone mounted on a cylinder, as shown in Fig. 13.8. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take π = 3.14)
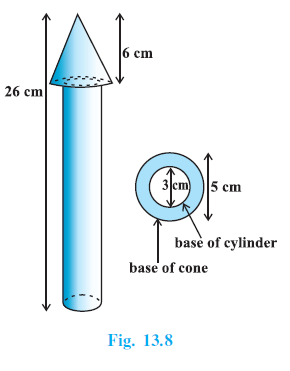
Answer:
Given:
A toy rocket shaped like a cone mounted on a cylinder.
Total height of the rocket = 26 cm.
Height of the conical part, $h_{cone} = 6$ cm.
Diameter of the base of the cone, $d_{cone} = 5$ cm.
Diameter of the base of the cylinder, $d_{cyl} = 3$ cm.
Conical portion is painted orange.
Cylindrical portion is painted yellow.
Value of $\pi = 3.14$.
To Find:
1. The area painted orange.
2. The area painted yellow.
Solution:
Dimensions:
Radius of the conical part, $r_{cone} = \frac{d_{cone}}{2} = \frac{5}{2} = 2.5$ cm.
Radius of the cylindrical part, $r_{cyl} = \frac{d_{cyl}}{2} = \frac{3}{2} = 1.5$ cm.
Height of the conical part, $h_{cone} = 6$ cm.
Height of the cylindrical part, $h_{cyl} = \text{Total height} - h_{cone} = 26 - 6 = 20$ cm.
Slant height of the conical part ($l_{cone}$):
$l_{cone} = \sqrt{r_{cone}^2 + h_{cone}^2}$
$l_{cone} = \sqrt{(2.5)^2 + (6)^2}$
$l_{cone} = \sqrt{6.25 + 36} = \sqrt{42.25}$
$l_{cone} = 6.5$ cm.
Area painted Orange:
The orange area includes the Curved Surface Area (CSA) of the cone and the area of the base ring of the cone (Base area of cone - Base area of cylinder).
CSA of cone = $\pi r_{cone} l_{cone}$
CSA of cone = $3.14 \times 2.5 \times 6.5$
CSA of cone = $3.14 \times 16.25 = 51.025$ cm$^2$.
Base area of cone = $\pi r_{cone}^2$
Base area of cone = $3.14 \times (2.5)^2 = 3.14 \times 6.25 = 19.625$ cm$^2$.
Base area of cylinder = $\pi r_{cyl}^2$
Base area of cylinder = $3.14 \times (1.5)^2 = 3.14 \times 2.25 = 7.065$ cm$^2$.
Area of the base ring of the cone = Base area of cone - Base area of cylinder
Area of base ring = $19.625 - 7.065 = 12.56$ cm$^2$.
Total area painted orange = CSA of cone + Area of base ring
Area (Orange) = $51.025 + 12.56 = 63.585$ cm$^2$.
Area painted Yellow:
The yellow area includes the Curved Surface Area (CSA) of the cylinder and the area of the bottom base of the cylinder.
CSA of cylinder = $2 \pi r_{cyl} h_{cyl}$
CSA of cylinder = $2 \times 3.14 \times 1.5 \times 20$
CSA of cylinder = $6.28 \times 30 = 188.4$ cm$^2$.
Area of the bottom base of cylinder = $\pi r_{cyl}^2 = 7.065$ cm$^2$ (calculated previously).
Total area painted yellow = CSA of cylinder + Area of bottom base
Area (Yellow) = $188.4 + 7.065 = 195.465$ cm$^2$.
Hence,
The area of the rocket painted orange is 63.585 cm$^2$.
The area of the rocket painted yellow is 195.465 cm$^2$.
Example 4. Mayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end (see Fig. 13.9). The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the bird-bath. (Take π = $\frac{22}{7}$ )
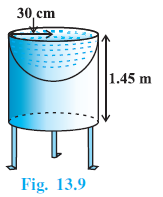
Answer:
Given:
Shape of the bird-bath: Cylinder with a hemispherical depression at one end.
Height of the cylinder, $h = 1.45$ m.
Radius of the cylinder (and hemisphere), $r = 30$ cm.
Value of $\pi = \frac{22}{7}$.
To Find:
The total surface area (TSA) of the bird-bath.
Solution:
First, ensure the units are consistent. Convert the height to centimeters.
Height $h = 1.45 \text{ m} = 1.45 \times 100 \text{ cm} = 145$ cm.
Radius $r = 30$ cm.
The total surface area of the bird-bath includes the Curved Surface Area (CSA) of the cylinder and the inner surface area of the hemispherical depression (which is the CSA of the hemisphere).
The base of the cylinder is usually considered part of the TSA, but in the context of a bird-bath, often the calculation focuses on the area exposed to water or the environment, which is the outer wall and the inner depression. Let's calculate based on this interpretation (CSA of cylinder + CSA of hemisphere).
Calculate the CSA of the cylinder:
CSA$_{cylinder}$ = $2 \pi r h$
CSA$_{cylinder}$ = $2 \times \frac{22}{7} \times 30 \times 145$
CSA$_{cylinder}$ = $\frac{44 \times 4350}{7} = \frac{191400}{7}$ cm$^2$.
Calculate the CSA of the hemisphere:
CSA$_{hemisphere}$ = $2 \pi r^2$
CSA$_{hemisphere}$ = $2 \times \frac{22}{7} \times (30)^2$
CSA$_{hemisphere}$ = $2 \times \frac{22}{7} \times 900$
CSA$_{hemisphere}$ = $\frac{44 \times 900}{7} = \frac{39600}{7}$ cm$^2$.
Calculate the Total Surface Area (TSA) of the bird-bath:
TSA = CSA$_{cylinder}$ + CSA$_{hemisphere}$
TSA = $\frac{191400}{7} + \frac{39600}{7}$
TSA = $\frac{191400 + 39600}{7} = \frac{231000}{7}$
TSA = $33000$ cm$^2$.
Converting the area to square meters:
TSA = $33000 \text{ cm}^2 = \frac{33000}{100 \times 100} \text{ m}^2 = 3.3 \text{ m}^2$.
Hence, the total surface area of the bird-bath is 33000 cm$^2$ or 3.3 m$^2$.
Exercise 13.1
Unless stated otherwise, take π = $\frac{22}{7}$
Question 1. 2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
Answer:
Given:
Two cubes are joined end to end.
Volume of each cube = 64 cm$^3$.
To Find:
The surface area of the resulting cuboid.
Solution:
Let the side length of each cube be $s$.
Volume of a cube = $s^3$.
Given, Volume = 64 cm$^3$.
$s^3 = 64$
$s = \sqrt[3]{64}$
$s = 4$ cm.
So, the edge of each cube is 4 cm.
When two such cubes are joined end to end, they form a cuboid.
The dimensions of the resulting cuboid will be:
Length ($L$) = Side of first cube + Side of second cube = $s + s = 4 + 4 = 8$ cm.
Breadth ($B$) = Side of cube = $s = 4$ cm.
Height ($H$) = Side of cube = $s = 4$ cm.
The surface area of a cuboid is given by the formula:
Surface Area = $2(LB + BH + HL)$
Substitute the values of $L$, $B$, and $H$:
Surface Area = $2((8)(4) + (4)(4) + (4)(8))$
Surface Area = $2(32 + 16 + 32)$
Surface Area = $2(80)$
Surface Area = $160$ cm$^2$.
Hence, the surface area of the resulting cuboid is 160 cm$^2$.
Question 2. A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
Answer:
Given:
Vessel is in the form of a hollow hemisphere mounted by a hollow cylinder.
Diameter of the hemisphere = 14 cm
Total height of the vessel = 13 cm
To Find:
The inner surface area of the vessel.
Solution:
The vessel consists of a hollow hemisphere and a hollow cylinder.
The diameter of the hemisphere is given as 14 cm.
Radius of the hemisphere, $r$ = $\frac{\text{Diameter}}{2}$.
$r = \frac{14}{2}$ cm
Radius of hemisphere, $r = 7$ cm.
... (i)
Since the cylinder is mounted on the hemisphere, the radius of the base of the cylinder is the same as the radius of the hemisphere.
Radius of the base of the cylinder, $r_c = r = 7$ cm.
The total height of the vessel is 13 cm.
The height of the hemispherical part is equal to its radius, which is 7 cm.
Height of the cylindrical part, $h$ = Total height - Height of hemisphere
$h = 13 \text{ cm} - 7 \text{ cm}$
Height of cylinder, $h = 6$ cm.
... (ii)
The inner surface area of the vessel is the sum of the inner surface area of the hemisphere and the inner surface area of the cylinder.
Inner surface area of hollow hemisphere = Curved Surface Area of hemisphere
CSA of hemisphere $= 2\pi r^2$.
... (iii)
Inner surface area of hollow cylinder = Curved Surface Area of cylinder (since it is hollow and mounted on the hemisphere, its base is covered by the hemisphere and the top is open)
CSA of cylinder $= 2\pi r h$.
... (iv)
Total inner surface area of the vessel = CSA of hemisphere + CSA of cylinder
Total Area $= 2\pi r^2 + 2\pi r h$
Total Area $= 2\pi r (r + h)$
Substituting the values from (i) and (ii):
Total Area $= 2\pi (7) (7 + 6)$
Total Area $= 14\pi (13)$
Total Area $= 182\pi$ cm$^2$
Using the value $\pi = \frac{22}{7}$:
Total Area $= 182 \times \frac{22}{7}$
Total Area $= \frac{\cancel{182}^{26} \times 22}{\cancel{7}_{1}}$
Total Area $= 26 \times 22$
Total Area $= 572$
So, the inner surface area of the vessel is 572 cm$^2$.
Final Answer:
The inner surface area of the vessel is $572 \text{ cm}^2$.
Question 3. A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Answer:
Given:
Toy is in the form of a cone mounted on a hemisphere.
Radius of the cone = 3.5 cm
Radius of the hemisphere = same as cone radius = 3.5 cm
Total height of the toy = 15.5 cm
To Find:
The total surface area of the toy.
Solution:
The toy consists of a cone and a hemisphere mounted on it.
Radius of the hemisphere, $r = 3.5$ cm.
Radius of the base of the cone, $r_c = 3.5$ cm.
The height of the hemispherical part is equal to its radius, which is 3.5 cm.
The total height of the toy is 15.5 cm.
Height of the conical part, $h$ = Total height of toy - Height of hemisphere
$h = 15.5 \text{ cm} - 3.5 \text{ cm}$
Height of cone, $h = 12$ cm.
... (i)
To find the total surface area of the toy, we need the curved surface area (CSA) of the hemisphere and the curved surface area (CSA) of the cone. The base of the cone is not included in the total surface area because it is covered by the hemisphere.
CSA of hemisphere $= 2\pi r^2$
To find the CSA of the cone, we need the slant height ($l$) of the cone.
The formula for slant height is $l = \sqrt{r^2 + h^2}$.
Substitute the values of $r$ and $h$ from (i):
$l = \sqrt{(3.5)^2 + (12)^2}$
$l = \sqrt{(3.5 \times 3.5) + (12 \times 12)}$
$3.5 \times 3.5 = 12.25$
$12 \times 12 = 144$
$l = \sqrt{12.25 + 144}$
$l = \sqrt{156.25}$
To find the square root of 156.25:
$\sqrt{156.25} = \sqrt{\frac{15625}{100}} = \frac{\sqrt{15625}}{\sqrt{100}} = \frac{125}{10} = 12.5$
Or using long division method:
$\begin{array}{c|cc} & 1\ 2\ . \ 5 & \\ \hline \phantom{()} 1 & \overline{1} \; \overline{56} \; . \overline{25} \\ + \; 1 & 1\phantom{(........)} \\ \hline \phantom{()} 2 \; 2 & 0 \; 56 \phantom{(.....)} \\ \phantom{()} +2 & 44 \phantom{(...)} \\ \hline \phantom{()} 24 \; 5 & 12 \; 25 \\ \phantom{()} +5 & 1225 \\ \hline \phantom{()} 250 & 0 \end{array}$
Slant height of cone, $l = 12.5$ cm.
... (ii)
CSA of cone $= \pi r l$
Total surface area of the toy = CSA of hemisphere + CSA of cone
Total Area $= 2\pi r^2 + \pi r l$
Total Area $= \pi r (2r + l)$
Substitute the values of $r$ and $l$ from (i) and (ii):
Using $r = 3.5 = \frac{7}{2}$ cm and $l = 12.5 = \frac{25}{2}$ cm.
Total Area $= \pi \times \frac{7}{2} \times \left(2 \times \frac{7}{2} + \frac{25}{2}\right)$
Total Area $= \pi \times \frac{7}{2} \times \left(7 + \frac{25}{2}\right)$
Total Area $= \pi \times \frac{7}{2} \times \left(\frac{14}{2} + \frac{25}{2}\right)$
Total Area $= \pi \times \frac{7}{2} \times \left(\frac{14 + 25}{2}\right)$
Total Area $= \pi \times \frac{7}{2} \times \frac{39}{2}$
Total Area $= \frac{273\pi}{4}$ cm$^2$
Using the value $\pi = \frac{22}{7}$:
Total Area $= \frac{273}{4} \times \frac{22}{7}$
Total Area $= \frac{\cancel{273}^{39} \times \cancel{22}^{11}}{\cancel{4}_{2} \times \cancel{7}_{1}}$
Total Area $= \frac{39 \times 11}{2}$
$39 \times 11 = 429$
Total Area $= \frac{429}{2}$
Total Area $= 214.5$
So, the total surface area of the toy is 214.5 cm$^2$.
Final Answer:
The total surface area of the toy is $214.5 \text{ cm}^2$.
Question 4. A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
Answer:
Given:
Cubical block of side 7 cm.
A hemisphere surmounts the cubical block.
To Find:
1. The greatest diameter the hemisphere can have.
2. The surface area of the solid.
Solution:
The cubical block has a side length of 7 cm.
When a hemisphere surmounts the cubical block, for the diameter to be the greatest possible, the base of the hemisphere must be a circle that covers the top face of the cube precisely. This means the diameter of the hemisphere's base is equal to the side length of the square top face of the cube.
Side of the cube = 7 cm.
(Given)
So, the greatest diameter the hemisphere can have is equal to the side length of the cube.
Greatest diameter of hemisphere $= 7$ cm.
... (i)
The radius of the hemisphere is half of its diameter.
Radius of hemisphere, $r = \frac{7}{2} = 3.5$ cm.
... (ii)
Now, we need to find the surface area of the solid.
The solid consists of the cubical block and the hemisphere surmounting it.
The surface area of the solid is the sum of the surface areas of all visible parts.
This includes:
1. The surface area of the cube excluding the area covered by the base of the hemisphere.
2. The curved surface area of the hemisphere.
Surface area of the cube $= 6 \times (\text{side})^2 = 6 \times (7 \text{ cm})^2 = 6 \times 49 \text{ cm}^2 = 294 \text{ cm}^2$.
The top face of the cube has a square area $= (\text{side})^2 = 7^2 = 49 \text{ cm}^2$.
The base of the hemisphere is a circle with radius $r = 3.5$ cm.
Area of the base of the hemisphere $= \pi r^2 = \pi (3.5)^2 = \pi (\frac{7}{2})^2 = \pi \times \frac{49}{4} \text{ cm}^2$.
Area of the cube exposed = (Total surface area of cube) - (Area covered by hemisphere base)
However, a simpler approach is to consider the surface area as:
Surface Area of Solid = (Area of 5 faces of the cube) + (Area of the top face of the cube excluding the base of the hemisphere) + (Curved surface area of the hemisphere)
Surface Area of Solid = $5 \times (\text{side})^2 + [(\text{side})^2 - \pi r^2] + 2\pi r^2$
Surface Area of Solid = $6 \times (\text{side})^2 - \pi r^2 + 2\pi r^2$
Surface Area of Solid = $6 \times (\text{side})^2 + \pi r^2$
Substitute side = 7 cm and $r = \frac{7}{2}$ cm:
Surface Area of Solid $= 6 \times (7)^2 + \pi \times \left(\frac{7}{2}\right)^2$
Surface Area of Solid $= 6 \times 49 + \pi \times \frac{49}{4}$
Surface Area of Solid $= 294 + \frac{49}{4}\pi$ cm$^2$.
Using the value $\pi = \frac{22}{7}$:
Surface Area of Solid $= 294 + \frac{49}{4} \times \frac{22}{7}$
Surface Area of Solid $= 294 + \frac{\cancel{49}^{7} \times \cancel{22}^{11}}{\cancel{4}_{2} \times \cancel{7}_{1}}$
Surface Area of Solid $= 294 + \frac{7 \times 11}{2}$
Surface Area of Solid $= 294 + \frac{77}{2}$
Surface Area of Solid $= 294 + 38.5$
Surface Area of Solid $= 332.5$
So, the surface area of the solid is 332.5 cm$^2$.
Final Answer:
The greatest diameter the hemisphere can have is $7 \text{ cm}$.
The surface area of the solid is $332.5 \text{ cm}^2$.
Question 5. A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Answer:
Given:
A cubical wooden block with edge length equal to $l$.
A hemispherical depression is cut out from one face.
The diameter of the hemisphere is equal to the edge of the cube, which is $l$.
To Find:
The surface area of the remaining solid.
Solution:
The edge length of the cubical block is $l$.
Edge of cube $= l$.
(Given)
The diameter of the hemispherical depression is equal to the edge of the cube.
Diameter of hemisphere $= l$.
(Given)
The radius of the hemisphere is half of its diameter.
Radius of hemisphere, $r = \frac{l}{2}$.
... (i)
The surface area of the remaining solid consists of the following parts:
1. The surface area of the five faces of the cube that are not cut.
2. The surface area of the face from which the hemisphere is cut, minus the circular area of the hemisphere's base.
3. The curved surface area of the hemispherical depression.
Surface area of the cube = $6 \times (\text{edge})^2 = 6l^2$.
Area of each face of the cube $= l^2$.
Area of the circular base of the hemisphere $= \pi r^2 = \pi \left(\frac{l}{2}\right)^2 = \pi \frac{l^2}{4}$.
Curved surface area of the hemisphere $= 2\pi r^2 = 2\pi \left(\frac{l}{2}\right)^2 = 2\pi \frac{l^2}{4} = \pi \frac{l^2}{2}$.
Surface area of the remaining solid = (Surface area of cube) - (Area of base of hemisphere) + (Curved surface area of hemisphere)
Surface Area $= 6l^2 - \pi r^2 + 2\pi r^2$
Surface Area $= 6l^2 + \pi r^2$
Substitute the value of $r$ from (i):
Surface Area $= 6l^2 + \pi \left(\frac{l}{2}\right)^2$
Surface Area $= 6l^2 + \pi \frac{l^2}{4}$
We can take $l^2$ common or express the term with a common denominator.
Surface Area $= \frac{4 \times 6l^2}{4} + \frac{\pi l^2}{4}$
Surface Area $= \frac{24l^2 + \pi l^2}{4}$
Surface Area $= \frac{l^2(24 + \pi)}{4}$
Alternatively, factoring out $l^2$ directly:
Surface Area $= l^2 \left(6 + \frac{\pi}{4}\right)$
Both expressions represent the surface area of the remaining solid.
Final Answer:
The surface area of the remaining solid is $\frac{l^2(24 + \pi)}{4}$ square units or $l^2 \left(6 + \frac{\pi}{4}\right)$ square units.
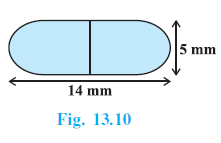
Question 6. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see Fig. 13.10). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.
Answer:
Given:
Medicine capsule shape: cylinder with two hemispheres stuck to each end.
Total length of the capsule = 14 mm
Diameter of the capsule = 5 mm
To Find:
The surface area of the capsule.
Solution:
The capsule is composed of a cylinder and two hemispheres of the same diameter.
The diameter of the capsule is 5 mm.
The radius of the capsule (hemisphere and cylinder) is half of the diameter.
Radius, $r = \frac{\text{Diameter}}{2} = \frac{5}{2} = 2.5$ mm.
Radius, $r = 2.5$ mm.
... (i)
The total length of the capsule is 14 mm.
The length of each hemispherical part is equal to its radius, which is 2.5 mm.
The length of the cylindrical part is the total length minus the lengths of the two hemispheres.
Height of the cylindrical part, $h$ = Total length - (Radius of one hemisphere) - (Radius of the other hemisphere)
$h = 14 \text{ mm} - 2.5 \text{ mm} - 2.5 \text{ mm}$
$h = 14 \text{ mm} - 5 \text{ mm}$
Height of cylinder, $h = 9$ mm.
... (ii)
The surface area of the capsule is the sum of the curved surface area (CSA) of the two hemispheres and the curved surface area of the cylinder.
CSA of one hemisphere $= 2\pi r^2$.
CSA of two hemispheres $= 2 \times (2\pi r^2) = 4\pi r^2$.
CSA of cylinder $= 2\pi r h$.
Total Surface Area of capsule = (CSA of two hemispheres) + (CSA of cylinder)
Total Area $= 4\pi r^2 + 2\pi r h$
We can factor out $2\pi r$ from the expression:
Total Area $= 2\pi r (2r + h)$
Substitute the values of $r$ and $h$ from (i) and (ii):
Total Area $= 2\pi (2.5 \text{ mm}) (2 \times 2.5 \text{ mm} + 9 \text{ mm})$
Total Area $= 2\pi (2.5) (5 + 9)$
Total Area $= 5\pi (14)$
Total Area $= 70\pi$ mm$^2$.
Using the value $\pi = \frac{22}{7}$:
Total Area $= 70 \times \frac{22}{7}$
Total Area $= \frac{\cancel{70}^{10} \times 22}{\cancel{7}_{1}}$
Total Area $= 10 \times 22$
Total Area $= 220$
So, the surface area of the medicine capsule is 220 mm$^2$.
Final Answer:
The surface area of the medicine capsule is $220 \text{ mm}^2$.
Question 7. A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of ₹ 500 per m2 . (Note that the base of the tent will not be covered with canvas.)
Answer:
Given:
Tent shape: cylinder surmounted by a conical top.
Height of the cylindrical part, $h_c = 2.1$ m.
Diameter of the cylindrical part = 4 m.
Slant height of the conical top, $l = 2.8$ m.
Cost of canvas = $\textsf{₹} \$ 500$ per m$^2$.
To Find:
1. The area of the canvas used for making the tent.
2. The cost of the canvas.
Solution:
The tent consists of a cylindrical part and a conical top. The diameter of the cylindrical part is 4 m.
Radius of the base of the cylindrical part, $r = \frac{\text{Diameter}}{2} = \frac{4}{2}$ m.
Radius, $r = 2$ m.
... (i)
The conical top surmounts the cylindrical part, so the base of the cone has the same diameter as the cylinder.
Radius of the base of the cone is also $r = 2$ m.
The height of the cylindrical part is given as $h_c = 2.1$ m.
The slant height of the conical top is given as $l = 2.8$ m.
The area of the canvas used for making the tent is the sum of the curved surface area (CSA) of the cylindrical part and the curved surface area of the conical part. The base of the tent is not covered with canvas.
CSA of the cylindrical part $= 2\pi r h_c$.
CSA of the conical part $= \pi r l$.
Total area of canvas = CSA of cylinder + CSA of cone
Total Area $= 2\pi r h_c + \pi r l$
We can factor out $\pi r$ from the expression:
Total Area $= \pi r (2h_c + l)$
Substitute the values from (i) and the given values of $h_c$ and $l$:
Total Area $= \pi (2 \text{ m}) (2 \times 2.1 \text{ m} + 2.8 \text{ m})$
Total Area $= 2\pi (4.2 + 2.8)$ m$^2$
Total Area $= 2\pi (7)$ m$^2$
Total Area $= 14\pi$ m$^2$.
Using the value $\pi = \frac{22}{7}$:
Total Area $= 14 \times \frac{22}{7}$ m$^2$
Total Area $= \frac{\cancel{14}^{2} \times 22}{\cancel{7}_{1}}$ m$^2$
Total Area $= 2 \times 22$ m$^2$
Total Area $= 44$ m$^2$.
... (ii)
Now, we need to find the cost of the canvas.
Rate of canvas = $\textsf{₹} \$ 500$ per m$^2$.
Cost of canvas = Total Area $\times$ Rate per m$^2$
Cost $= 44 \text{ m}^2 \times \textsf{₹} \$ 500 / \text{m}^2$
Cost $= 44 \times 500 \textsf{₹}$
Cost $= 22000 \textsf{₹}$.
Final Answer:
The area of the canvas used for making the tent is $44 \text{ m}^2$.
The cost of the canvas of the tent is $\textsf{₹} \$ 22000$.
Question 8. From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2 .
Answer:
Given:
Solid cylinder with height $h = 2.4$ cm and diameter $d = 1.4$ cm.
A conical cavity of the same height and diameter is hollowed out from the cylinder.
To Find:
The total surface area of the remaining solid to the nearest cm$^2$.
Solution:
The remaining solid consists of:
- The base of the cylinder.
- The curved surface area of the cylinder.
- The curved surface area of the conical cavity.
Diameter of the cylinder = Diameter of the cone = 1.4 cm.
Radius, $r = \frac{\text{Diameter}}{2} = \frac{1.4}{2}$ cm.
Radius, $r = 0.7$ cm.
... (i)
Height of the cylinder, $h = 2.4$ cm.
Height of the conical cavity, $h = 2.4$ cm.
To find the total surface area, we need the curved surface area of the cylinder and the curved surface area of the cone. We also need the area of the base of the cylinder.
Area of the base of the cylinder $= \pi r^2$.
Curved Surface Area of the cylinder $= 2\pi r h$.
Curved Surface Area of the cone $= \pi r l$, where $l$ is the slant height of the cone.
First, calculate the slant height $l$ of the cone using the formula $l = \sqrt{r^2 + h^2}$.
Substitute the values of $r$ and $h$:
$l = \sqrt{(0.7)^2 + (2.4)^2}$
$l = \sqrt{0.49 + 5.76}$
$l = \sqrt{6.25}$
$\sqrt{6.25} = 2.5$.
Slant height of cone, $l = 2.5$ cm.
... (ii)
Total surface area of the remaining solid = (Area of base of cylinder) + (CSA of cylinder) + (CSA of cone)
Total Area $= \pi r^2 + 2\pi r h + \pi r l$
Factor out $\pi r$:
Total Area $= \pi r (r + 2h + l)$
Substitute the values of $r, h,$ and $l$ from (i), the given information, and (ii):
Total Area $= \pi (0.7) (0.7 + 2 \times 2.4 + 2.5)$
Total Area $= \pi (0.7) (0.7 + 4.8 + 2.5)$
Total Area $= \pi (0.7) (8.0)$
Total Area $= 5.6 \pi$ cm$^2$.
Using the value $\pi = \frac{22}{7}$:
Total Area $= 5.6 \times \frac{22}{7}$
Total Area $= \frac{5.6}{7} \times 22$
Total Area $= 0.8 \times 22$
Total Area $= 17.6$ cm$^2$.
We are asked to find the total surface area to the nearest cm$^2$.
$17.6$ cm$^2$ rounded to the nearest whole number is 18 cm$^2$.
Final Answer:
The total surface area of the remaining solid to the nearest cm$^2$ is $18 \text{ cm}^2$.
Question 9. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 13.11. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.

Answer:
Given:
Wooden article made by scooping out a hemisphere from each end of a solid cylinder.
Height of the cylinder, $h = 10$ cm.
Radius of the base of the cylinder, $r = 3.5$ cm.
To Find:
The total surface area of the article.
Solution:
The article is formed by a cylinder with two hemispheres removed from its ends. The surface area of the remaining solid consists of the curved surface area of the cylinder and the curved surface area of the two hemispherical depressions.
The radius of the base of the cylinder is 3.5 cm. Since the hemispheres are scooped out from the ends, the radius of each hemisphere is the same as the radius of the cylinder's base.
Radius of cylinder and hemisphere, $r = 3.5$ cm.
... (i)
The height of the cylinder is given as 10 cm.
Height of cylinder, $h = 10$ cm.
... (ii)
The total surface area of the article is the sum of the curved surface area (CSA) of the cylinder and the curved surface area of the two hemispheres.
CSA of cylinder $= 2\pi r h$.
CSA of one hemisphere $= 2\pi r^2$.
CSA of two hemispheres $= 2 \times (2\pi r^2) = 4\pi r^2$.
Total Surface Area of the article = CSA of cylinder + CSA of two hemispheres
Total Area $= 2\pi r h + 4\pi r^2$
We can factor out $2\pi r$ from the expression:
Total Area $= 2\pi r (h + 2r)$
Substitute the values of $r$ and $h$ from (i) and (ii):
$r = 3.5 = \frac{7}{2}$ cm.
Total Area $= 2\pi \left(\frac{7}{2}\right) \left(10 + 2 \times \frac{7}{2}\right)$
Total Area $= 7\pi (10 + 7)$
Total Area $= 7\pi (17)$
Total Area $= 119\pi$ cm$^2$.
Using the value $\pi = \frac{22}{7}$:
Total Area $= 119 \times \frac{22}{7}$ cm$^2$
Total Area $= \frac{\cancel{119}^{17} \times 22}{\cancel{7}_{1}}$ cm$^2$
Total Area $= 17 \times 22$ cm$^2$
$17 \times 22 = 374$
Total Area $= 374$ cm$^2$.
So, the total surface area of the wooden article is 374 cm$^2$.
Final Answer:
The total surface area of the article is $374 \text{ cm}^2$.
Example 5 to 7 (Before Exercise 13.2)
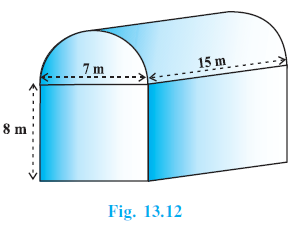
Example 5. Shanta runs an industry in a shed which is in the shape of a cuboid surmounted by a half cylinder (see Fig. 13.12). If the base of the shed is of dimension 7 m × 15 m, and the height of the cuboidal portion is 8 m, find the volume of air that the shed can hold. Further, suppose the machinery in the shed occupies a total space of 300 m3 , and there are 20 workers, each of whom occupy about 0.08 m3 space on an average. Then, how much air is in the shed? (Take π = $\frac{22}{7}$ )
Answer:
Given:
Shed is in the shape of a cuboid surmounted by a half cylinder.
Base dimensions of the cuboidal portion = 7 m $\times$ 15 m.
Height of the cuboidal portion, $h_c = 8$ m.
The half cylinder surmounts the cuboid's base (7 m $\times$ 15 m face). Thus, the diameter of the semicircular base of the half cylinder is 7 m, and its length is 15 m.
Volume occupied by machinery = 300 m$^3$.
Number of workers = 20.
Space occupied by each worker = 0.08 m$^3$ (on average).
Value of $\pi = \frac{22}{7}$.
To Find:
1. The volume of air that the shed can hold (total volume of the shed).
2. The volume of air remaining in the shed after accounting for machinery and workers.
Solution:
The shed consists of a cuboidal part and a semicylindrical part.
For the cuboidal part:
Length, $l = 15$ m.
Width, $w = 7$ m.
Height, $h_c = 8$ m.
Volume of the cuboidal part, $V_{cuboid} = l \times w \times h_c = 15 \times 7 \times 8$ m$^3$.
$V_{cuboid} = 105 \times 8 = 840$ m$^3$.
For the semicylindrical part:
The diameter of the semicircular base is the width of the cuboid base, $d = 7$ m.
Radius of the semicylinder, $r = \frac{d}{2} = \frac{7}{2} = 3.5$ m.
The length of the semicylinder is the length of the cuboid base, which acts as the height of the cylinder in the volume formula, $h_{sc} = 15$ m.
Volume of the semicylindrical part, $V_{semicylinder} = \frac{1}{2} \times (\text{Volume of a cylinder})$.
Volume of a cylinder $= \pi r^2 h_{sc}$.
$V_{semicylinder} = \frac{1}{2} \pi r^2 h_{sc} = \frac{1}{2} \times \frac{22}{7} \times (3.5)^2 \times 15$ m$^3$.
$V_{semicylinder} = \frac{1}{2} \times \frac{22}{7} \times (\frac{7}{2})^2 \times 15 = \frac{1}{2} \times \frac{22}{7} \times \frac{49}{4} \times 15$ m$^3$.
$V_{semicylinder} = \frac{1}{\cancel{2}_1} \times \frac{\cancel{22}^{11}}{\cancel{7}_1} \times \frac{\cancel{49}^7}{\cancel{4}_2} \times 15 = \frac{11 \times 7 \times 15}{2 \times 2} = \frac{77 \times 15}{4} = \frac{1155}{4}$ m$^3$.
$V_{semicylinder} = 288.75$ m$^3$.
The volume of air that the shed can hold is the total volume of the shed.
Total volume of shed, $V_{shed} = V_{cuboid} + V_{semicylinder}$.
$V_{shed} = 840 \text{ m}^3 + 288.75 \text{ m}^3 = 1128.75 \text{ m}^3$.
Next, we need to find the volume of air remaining after accounting for machinery and workers.
Volume occupied by machinery = 300 m$^3$.
Volume occupied by 20 workers = Number of workers $\times$ Space per worker.
Volume occupied by workers $= 20 \times 0.08 = 1.6$ m$^3$.
Total space occupied by machinery and workers $= 300 \text{ m}^3 + 1.6 \text{ m}^3 = 301.6 \text{ m}^3$.
Volume of air in the shed = Total volume of shed - Total space occupied by machinery and workers.
Volume of air $= 1128.75 \text{ m}^3 - 301.6 \text{ m}^3 = 827.15 \text{ m}^3$.
Final Answer:
The volume of air that the shed can hold is $1128.75 \text{ m}^3$.
The volume of air remaining in the shed is $827.15 \text{ m}^3$.
Example 6. A juice seller was serving his customers using glasses as shown in Fig. 13.13. The inner diameter of the cylindrical glass was 5 cm, but the bottom of the glass had a hemispherical raised portion which reduced the capacity of the glass. If the height of a glass was 10 cm, find the apparent capacity of the glass and its actual capacity. (Use π = 3.14.)

Answer:
Given:
Inner diameter of cylindrical glass = 5 cm.
Height of the glass, $h = 10$ cm.
Bottom has a hemispherical raised portion.
Diameter of the hemispherical raised portion = Inner diameter of glass = 5 cm.
Value of $\pi = 3.14$.
To Find:
1. Apparent capacity of the glass.
2. Actual capacity of the glass.
Solution:
The inner diameter of the cylindrical glass is 5 cm.
Radius of the cylindrical glass, $r = \frac{\text{Diameter}}{2} = \frac{5}{2}$ cm.
Radius, $r = 2.5$ cm.
... (i)
The height of the cylindrical glass is 10 cm.
Height of cylinder, $h = 10$ cm.
... (ii)
The apparent capacity of the glass is the volume of the cylindrical part assuming a flat bottom.
Apparent Capacity = Volume of Cylinder $= \pi r^2 h$.
Substitute the values from (i), (ii), and the given value of $\pi$:
Apparent Capacity $= 3.14 \times (2.5)^2 \times 10$ cm$^3$.
Apparent Capacity $= 3.14 \times (2.5 \times 2.5) \times 10$ cm$^3$.
$2.5 \times 2.5 = 6.25$.
Apparent Capacity $= 3.14 \times 6.25 \times 10$ cm$^3$.
Apparent Capacity $= 3.14 \times 62.5$ cm$^3$.
$3.14 \times 62.5 = 196.25$
Apparent Capacity $= 196.25$ cm$^3$.
... (iii)
The actual capacity is reduced by the volume of the hemispherical raised portion at the bottom.
The diameter of the hemisphere is 5 cm, so its radius is $r = 2.5$ cm (same as the cylinder's radius).
Volume of the hemispherical raised portion $= \frac{2}{3} \pi r^3$.
Substitute the values from (i) and the given value of $\pi$:
Volume of Hemisphere $= \frac{2}{3} \times 3.14 \times (2.5)^3$ cm$^3$.
$(2.5)^3 = 2.5 \times 2.5 \times 2.5 = 6.25 \times 2.5 = 15.625$.
Volume of Hemisphere $= \frac{2}{3} \times 3.14 \times 15.625$ cm$^3$.
$3.14 \times 15.625 = 49.0625$.
Volume of Hemisphere $= \frac{2}{3} \times 49.0625 = \frac{98.125}{3}$ cm$^3$.
Volume of Hemisphere $\approx 32.7083$ cm$^3$.
Actual Capacity = Apparent Capacity - Volume of Hemisphere.
Actual Capacity $= 196.25 \text{ cm}^3 - \frac{98.125}{3} \text{ cm}^3$.
To perform subtraction:
$196.25 = \frac{196.25 \times 3}{3} = \frac{588.75}{3}$.
Actual Capacity $= \frac{588.75}{3} - \frac{98.125}{3} = \frac{588.75 - 98.125}{3} = \frac{490.625}{3}$ cm$^3$.
Actual Capacity $\approx 163.54166...$ cm$^3$.
Rounding to two decimal places, the actual capacity is approximately 163.54 cm$^3$.
Final Answer:
The apparent capacity of the glass is $196.25 \text{ cm}^3$.
The actual capacity of the glass is approximately $163.54 \text{ cm}^3$.
Example 7. A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference of the volumes of the cylinder and the toy. (Take π = 3.14)
Answer:
Given:
Solid toy shape: hemisphere surmounted by a right circular cone.
Height of the cone, $h = 2$ cm.
Diameter of the base (cone and hemisphere) = 4 cm.
Value of $\pi = 3.14$.
To Find:
1. The volume of the toy.
2. The difference between the volumes of the circumscribing cylinder and the toy.
Solution:
The toy is a combination of a hemisphere and a cone with a common base.
The diameter of the base is 4 cm.
Radius of the base, $r = \frac{\text{Diameter}}{2} = \frac{4}{2}$ cm.
Radius, $r = 2$ cm.
... (i)
Height of the cone, $h = 2$ cm.
Radius of the hemisphere, $r = 2$ cm.
The volume of the toy is the sum of the volume of the cone and the volume of the hemisphere.
Volume of cone $= \frac{1}{3} \pi r^2 h$.
Volume of hemisphere $= \frac{2}{3} \pi r^3$.
Volume of Toy, $V_{toy} = \text{Volume of cone} + \text{Volume of hemisphere}$.
$V_{toy} = \frac{1}{3} \pi r^2 h + \frac{2}{3} \pi r^3$.
Factor out $\frac{1}{3} \pi r^2$:
$V_{toy} = \frac{1}{3} \pi r^2 (h + 2r)$.
Substitute the values of $r, h,$ and $\pi$:
$V_{toy} = \frac{1}{3} \times 3.14 \times (2)^2 \times (2 + 2 \times 2)$ cm$^3$.
$V_{toy} = \frac{1}{3} \times 3.14 \times 4 \times (2 + 4)$ cm$^3$.
$V_{toy} = \frac{1}{3} \times 3.14 \times 4 \times 6$ cm$^3$.
$V_{toy} = \frac{1}{3} \times 3.14 \times 24$ cm$^3$.
$V_{toy} = 3.14 \times \frac{\cancel{24}^8}{\cancel{3}_1}$ cm$^3$.
$V_{toy} = 3.14 \times 8$ cm$^3$.
$V_{toy} = 25.12$ cm$^3$.
Volume of Toy $= 25.12 \text{ cm}^3$.
... (ii)
Now, consider a right circular cylinder that circumscribes the toy.
The base of the cylinder will be the same as the base of the toy, so the radius of the cylinder, $R$, is equal to the radius of the toy's base, $r = 2$ cm.
Radius of cylinder, $R = 2$ cm.
... (iii)
The height of the circumscribing cylinder will be the total height of the toy, which is the sum of the height of the cone and the radius of the hemisphere.
Height of cylinder, $H = \text{Height of cone} + \text{Radius of hemisphere}$.
$H = 2 \text{ cm} + 2 \text{ cm}$.
Height of cylinder, $H = 4$ cm.
... (iv)
Volume of the circumscribing cylinder, $V_{cylinder} = \pi R^2 H$.
Substitute the values from (iii), (iv), and the given value of $\pi$:
$V_{cylinder} = 3.14 \times (2)^2 \times 4$ cm$^3$.
$V_{cylinder} = 3.14 \times 4 \times 4$ cm$^3$.
$V_{cylinder} = 3.14 \times 16$ cm$^3$.
$V_{cylinder} = 50.24$ cm$^3$.
Volume of Cylinder $= 50.24 \text{ cm}^3$.
... (v)
The difference of the volumes of the cylinder and the toy is $V_{difference} = V_{cylinder} - V_{toy}$.
Substitute the values from (v) and (ii):
$V_{difference} = 50.24 \text{ cm}^3 - 25.12 \text{ cm}^3$.
$V_{difference} = 25.12$ cm$^3$.
Final Answer:
The volume of the toy is $25.12 \text{ cm}^3$.
The difference of the volumes of the cylinder and the toy is $25.12 \text{ cm}^3$.
Exercise 13.2
Unless stated otherwise, take π = $\frac{22}{7}$
Question 1. A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
Answer:
Given:
Solid is in the shape of a cone standing on a hemisphere.
Radius of hemisphere, $r = 1$ cm.
Radius of cone, $r_c = 1$ cm.
Height of cone, $h = $ radius of cone.
To Find:
The volume of the solid in terms of $\pi$.
Solution:
The solid is a combination of a hemisphere and a cone.
The radii of both the hemisphere and the cone are equal to 1 cm.
Radius, $r = 1$ cm.
... (i)
The height of the cone is equal to its radius.
Height of cone, $h = r = 1$ cm.
... (ii)
The volume of the solid is the sum of the volume of the cone and the volume of the hemisphere.
Volume of solid $= \text{Volume of cone} + \text{Volume of hemisphere}$.
Volume of cone $= \frac{1}{3} \pi r^2 h$.
Volume of hemisphere $= \frac{2}{3} \pi r^3$.
Substitute the values of $r$ and $h$ from (i) and (ii) into the formulas:
Volume of cone $= \frac{1}{3} \pi (1)^2 (1) = \frac{1}{3} \pi \times 1 \times 1 = \frac{1}{3} \pi$ cm$^3$.
Volume of hemisphere $= \frac{2}{3} \pi (1)^3 = \frac{2}{3} \pi \times 1 = \frac{2}{3} \pi$ cm$^3$.
Total Volume of solid $= \frac{1}{3} \pi + \frac{2}{3} \pi$
Total Volume $= \left(\frac{1}{3} + \frac{2}{3}\right) \pi$
Total Volume $= \left(\frac{1+2}{3}\right) \pi$
Total Volume $= \frac{3}{3} \pi$
Total Volume $= \pi$ cm$^3$.
... (iii)
The volume of the solid in terms of $\pi$ is $\pi$ cm$^3$.
Final Answer:
The volume of the solid is $\pi \text{ cm}^3$.
Question 2. Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
Answer:
Given:
Model shape: cylinder with two cones attached at its ends.
Diameter of the model = 3 cm.
Total length of the model = 12 cm.
Height of each cone = 2 cm.
To Find:
The volume of air contained in the model (volume of the solid).
Solution:
The model consists of a cylinder in the middle and two identical cones at its ends.
The diameter of the model is the diameter of the cylindrical part and the diameter of the base of each cone, which is 3 cm.
Radius, $r = \frac{\text{Diameter}}{2} = \frac{3}{2}$ cm.
Radius, $r = 1.5$ cm.
... (i)
The height of each cone is given as 2 cm.
Height of cone, $h_c = 2$ cm.
... (ii)
The total length of the model is 12 cm. This total length is the sum of the height of the cylinder and the heights of the two cones.
Total length = Height of Cone 1 + Height of Cylinder + Height of Cone 2.
Let $H$ be the height of the cylinder.
$12 \text{ cm} = h_c + H + h_c = 2h_c + H$.
Substitute the value of $h_c$ from (ii):
$12 = 2(2) + H$
$12 = 4 + H$
$H = 12 - 4$
Height of cylinder, $H = 8$ cm.
... (iii)
The volume of air contained in the model is the sum of the volumes of the two cones and the cylinder.
Volume of one cone $= \frac{1}{3} \pi r^2 h_c$.
Volume of cylinder $= \pi r^2 H$.
Total Volume of model $= 2 \times (\text{Volume of one cone}) + (\text{Volume of cylinder})$.
Total Volume $= 2 \times \frac{1}{3} \pi r^2 h_c + \pi r^2 H$.
Factor out $\pi r^2$:
Total Volume $= \pi r^2 \left(\frac{2}{3} h_c + H\right)$.
Substitute the values of $r, h_c,$ and $H$ from (i), (ii), and (iii):
Total Volume $= \pi (1.5)^2 \left(\frac{2}{3} \times 2 + 8\right)$ cm$^3$.
$1.5 = \frac{3}{2}$. So, $(1.5)^2 = \left(\frac{3}{2}\right)^2 = \frac{9}{4} = 2.25$.
Total Volume $= \pi (2.25) \left(\frac{4}{3} + 8\right)$ cm$^3$.
Combine the terms in the parenthesis:
$\frac{4}{3} + 8 = \frac{4}{3} + \frac{8 \times 3}{3} = \frac{4}{3} + \frac{24}{3} = \frac{4+24}{3} = \frac{28}{3}$.
Total Volume $= \pi (2.25) \left(\frac{28}{3}\right)$ cm$^3$.
Substitute $2.25 = \frac{9}{4}$:
Total Volume $= \pi \times \frac{9}{4} \times \frac{28}{3}$ cm$^3$.
Cancel common factors:
Total Volume $= \pi \times \frac{\cancel{9}^3}{\cancel{4}_1} \times \frac{\cancel{28}^7}{\cancel{3}_1}$ cm$^3$.
Total Volume $= \pi \times 3 \times 7$ cm$^3$.
Total Volume $= 21\pi$ cm$^3$.
The volume of air contained in the model is $21\pi$ cm$^3$.
Final Answer:
The volume of air contained in the model is $21\pi \text{ cm}^3$.
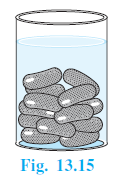
Question 3. A gulab jamun,contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns,each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (see Fig. 13.15).
Answer:
Given:
Shape of each gulab jamun: cylinder with two hemispherical ends.
Length of each gulab jamun = 5 cm.
Diameter of each gulab jamun = 2.8 cm.
Sugar syrup content = 30% of volume.
Number of gulab jamuns = 45.
To Find:
Approximately how much syrup is in 45 gulab jamuns.
Solution:
Each gulab jamun is a solid composed of a cylinder and two hemispheres.
The diameter of the gulab jamun is 2.8 cm. This is the diameter of the cylindrical part and the diameter of the hemispherical ends.
Radius, $r = \frac{\text{Diameter}}{2} = \frac{2.8}{2}$ cm.
Radius, $r = 1.4$ cm.
... (i)
The total length of the gulab jamun is 5 cm.
The length of each hemispherical part is equal to its radius, which is 1.4 cm.
The height of the cylindrical part, $h$, is the total length minus the radii of the two hemispheres.
$h = \text{Total length} - 2 \times \text{Radius of hemisphere}$
$h = 5 \text{ cm} - 2 \times 1.4 \text{ cm}$
$h = 5 \text{ cm} - 2.8 \text{ cm}$
Height of cylinder, $h = 2.2$ cm.
... (ii)
The volume of one gulab jamun is the sum of the volume of the cylindrical part and the volumes of the two hemispherical ends.
Volume of one gulab jamun, $V_{gj} = \text{Volume of cylinder} + 2 \times (\text{Volume of a hemisphere})$.
Volume of cylinder $= \pi r^2 h$.
Volume of a hemisphere $= \frac{2}{3} \pi r^3$.
$V_{gj} = \pi r^2 h + 2 \times \frac{2}{3} \pi r^3$
$V_{gj} = \pi r^2 h + \frac{4}{3} \pi r^3$
Factor out $\pi r^2$:
$V_{gj} = \pi r^2 \left(h + \frac{4}{3}r\right)$.
Substitute the values of $r$ and $h$ from (i) and (ii). Using $r = 1.4 = \frac{14}{10} = \frac{7}{5}$ and $h = 2.2 = \frac{22}{10} = \frac{11}{5}$.
$V_{gj} = \pi \left(\frac{7}{5}\right)^2 \left(\frac{11}{5} + \frac{4}{3} \times \frac{7}{5}\right)$ cm$^3$.
$V_{gj} = \pi \frac{49}{25} \left(\frac{11}{5} + \frac{28}{15}\right)$ cm$^3$.
Combine the terms in the parenthesis:
$\frac{11}{5} + \frac{28}{15} = \frac{11 \times 3}{5 \times 3} + \frac{28}{15} = \frac{33}{15} + \frac{28}{15} = \frac{33+28}{15} = \frac{61}{15}$.
$V_{gj} = \pi \frac{49}{25} \times \frac{61}{15}$ cm$^3$.
$V_{gj} = \frac{2989\pi}{375}$ cm$^3$.
Using $\pi = \frac{22}{7}$:
$V_{gj} = \frac{2989}{375} \times \frac{22}{7}$ cm$^3$.
$V_{gj} = \frac{\cancel{2989}^{427} \times 22}{375 \times \cancel{7}_1}$ cm$^3$.
$V_{gj} = \frac{427 \times 22}{375} = \frac{9394}{375}$ cm$^3$.
The total volume of 45 gulab jamuns is $45 \times V_{gj}$.
Total Volume $= 45 \times \frac{9394}{375}$ cm$^3$.
Cancel common factors:
Total Volume $= \frac{\cancel{45}^{3}}{\cancel{375}_{25}} \times 9394$ cm$^3$ (since $45 = 3 \times 15$ and $375 = 25 \times 15$).
Total Volume $= \frac{3}{25} \times 9394$ cm$^3$.
Total Volume $= \frac{28182}{25}$ cm$^3$.
Total Volume $= 1127.28$ cm$^3$.
The volume of sugar syrup is approximately 30% of the total volume of 45 gulab jamuns.
Volume of syrup $= 30\% \text{ of } 1127.28 \text{ cm}^3$
Volume of syrup $= 0.30 \times 1127.28$ cm$^3$
Volume of syrup $= 338.184$ cm$^3$.
Rounding to the nearest whole number as requested for an approximate value, the volume of syrup is 338 cm$^3$.
Final Answer:
Approximately, the volume of sugar syrup in 45 gulab jamuns is $338 \text{ cm}^3$.
Question 4. A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see Fig. 13.16).
Answer:
Given:
Pen stand shape: cuboid with four conical depressions.
Dimensions of cuboid: Length ($l$) = 15 cm, Width ($w$) = 10 cm, Height ($h_{cuboid}$) = 3.5 cm.
For each conical depression:
Radius ($r$) = 0.5 cm.
Depth (Height, $h_{cone}$) = 1.4 cm.
Number of conical depressions = 4.
To Find:
The volume of wood in the entire stand.
Solution:
The volume of wood in the stand is equal to the volume of the cuboid minus the total volume of the four conical depressions.
Volume of the cuboid $= l \times w \times h_{cuboid}$.
Volume of cuboid $= 15 \text{ cm} \times 10 \text{ cm} \times 3.5 \text{ cm}$.
Volume of cuboid $= 150 \times 3.5$ cm$^3$.
Volume of cuboid $= 525$ cm$^3$.
Volume of cuboid $= 525 \text{ cm}^3$.
... (i)
The conical depressions are identical. The volume of one conical depression is given by the formula $\frac{1}{3} \pi r^2 h_{cone}$.
Radius of cone, $r = 0.5 \text{ cm} = \frac{1}{2}$ cm.
Height of cone, $h_{cone} = 1.4 \text{ cm} = \frac{14}{10} = \frac{7}{5}$ cm.
Using $\pi = \frac{22}{7}$:
Volume of one conical depression $= \frac{1}{3} \pi r^2 h_{cone}$.
Volume of one cone $= \frac{1}{3} \times \frac{22}{7} \times \left(\frac{1}{2}\right)^2 \times \frac{7}{5}$
Volume of one cone $= \frac{1}{3} \times \frac{22}{7} \times \frac{1}{4} \times \frac{7}{5}$
Volume of one cone $= \frac{1}{3} \times \frac{22}{\cancel{7}_1} \times \frac{1}{4} \times \frac{\cancel{7}_1}{5}$
Volume of one cone $= \frac{22}{3 \times 4 \times 5} = \frac{22}{60} = \frac{11}{30}$ cm$^3$.
There are 4 such conical depressions. Total volume of the four conical depressions $= 4 \times (\text{Volume of one cone})$.
Total volume of 4 cones $= 4 \times \frac{11}{30}$ cm$^3$.
Total volume of 4 cones $= \frac{\cancel{4}^2 \times 11}{\cancel{30}_{15}}$ cm$^3$.
Total volume of 4 cones $= \frac{22}{15}$ cm$^3$.
... (ii)
Volume of wood in the pen stand = Volume of cuboid - Total volume of 4 conical depressions.
Volume of wood $= 525 \text{ cm}^3 - \frac{22}{15} \text{ cm}^3$.
To subtract, we find a common denominator, which is 15.
$525 = \frac{525 \times 15}{15} = \frac{7875}{15}$.
Volume of wood $= \frac{7875}{15} - \frac{22}{15}$ cm$^3$.
Volume of wood $= \frac{7875 - 22}{15}$ cm$^3$.
Volume of wood $= \frac{7853}{15}$ cm$^3$.
To express this as a decimal:
$\frac{7853}{15} \approx 523.5333...$ cm$^3$.
Rounding to two decimal places, we get 523.53 cm$^3$.
Final Answer:
The volume of wood in the entire stand is $\frac{7853}{15} \text{ cm}^3$ or approximately $523.53 \text{ cm}^3$.
Question 5. A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Answer:
Given:
Vessel shape: Inverted cone.
Height of cone, $H = 8$ cm.
Radius of top (base) of cone, $R = 5$ cm.
Vessel is filled with water up to the brim.
Lead shots are spheres.
Radius of each lead shot (sphere), $r = 0.5$ cm.
Volume of water overflowed = $\frac{1}{4}$ of the volume of the cone.
To Find:
The number of lead shots dropped in the vessel.
Solution:
The volume of the cone represents the initial volume of water in the vessel.
Volume of cone, $V_{cone} = \frac{1}{3} \pi R^2 H$.
Substitute the values of $R$ and $H$:
$V_{cone} = \frac{1}{3} \pi (5 \text{ cm})^2 (8 \text{ cm})$
$V_{cone} = \frac{1}{3} \pi (25) (8)$ cm$^3$
$V_{cone} = \frac{200\pi}{3}$ cm$^3$.
... (i)
When lead shots are dropped, water overflows. The volume of water that overflows is equal to the total volume of the lead shots submerged in the water.
Volume of water overflowed = $\frac{1}{4} \times V_{cone}$.
Substitute the value of $V_{cone}$ from (i):
Volume of overflowed water $= \frac{1}{4} \times \frac{200\pi}{3}$ cm$^3$.
Volume of overflowed water $= \frac{\cancel{200}^{50}\pi}{4 \times 3}$ cm$^3$.
Volume of overflowed water $= \frac{50\pi}{3}$ cm$^3$.
... (ii)
The radius of each spherical lead shot is 0.5 cm.
Radius of sphere, $r = 0.5 \text{ cm} = \frac{1}{2}$ cm.
Volume of a single sphere, $V_{sphere} = \frac{4}{3} \pi r^3$.
Substitute the value of $r$:
$V_{sphere} = \frac{4}{3} \pi \left(\frac{1}{2} \text{ cm}\right)^3$.
$V_{sphere} = \frac{4}{3} \pi \left(\frac{1}{8}\right)$ cm$^3$.
$V_{sphere} = \frac{\cancel{4}_1 \pi}{3 \times \cancel{8}_2}$ cm$^3$.
$V_{sphere} = \frac{\pi}{6}$ cm$^3$.
... (iii)
Let $N$ be the number of lead shots dropped in the vessel.
The total volume of the lead shots is $N \times V_{sphere}$.
This total volume is equal to the volume of the overflowed water.
Total volume of lead shots = Volume of overflowed water.
(By Archimedes' principle)
$N \times V_{sphere} = V_{overflowed\ water}$.
Substitute the values from (iii) and (ii):
$N \times \frac{\pi}{6} = \frac{50\pi}{3}$.
To find $N$, rearrange the equation:
$N = \frac{50\pi}{3} \div \frac{\pi}{6}$.
$N = \frac{50\pi}{3} \times \frac{6}{\pi}$.
$N = \frac{50 \times \cancel{\pi}}{\cancel{3}_1} \times \frac{\cancel{6}^2}{\cancel{\pi}_1}$.
$N = 50 \times 2$.
$N = 100$.
... (iv)
Thus, the number of lead shots dropped in the vessel is 100.
Final Answer:
The number of lead shots dropped in the vessel is 100.
Question 6. A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8g mass. (Use π = 3.14)
Answer:
Given:
Solid iron pole consists of a cylinder surmounted by another cylinder.
For the lower cylinder:
Height, $h_1 = 220$ cm.
Base diameter, $d_1 = 24$ cm.
For the upper cylinder:
Height, $h_2 = 60$ cm.
Radius, $r_2 = 8$ cm.
Mass of 1 cm$^3$ of iron $\approx 8$ g.
Use $\pi = 3.14$.
To Find:
The mass of the iron pole.
Solution:
The solid pole is a composite solid formed by two cylinders placed one on top of the other.
First, calculate the volume of the lower cylinder.
The base diameter is 24 cm, so the radius is $r_1 = \frac{24}{2}$ cm.
Radius of lower cylinder, $r_1 = 12$ cm.
... (i)
Height of lower cylinder, $h_1 = 220$ cm.
Volume of lower cylinder, $V_1 = \pi r_1^2 h_1$.
Substitute the values from (i) and the given height:
$V_1 = \pi (12 \text{ cm})^2 (220 \text{ cm})$.
$V_1 = \pi (144 \times 220)$ cm$^3$.
$V_1 = 31680\pi$ cm$^3$.
... (ii)
Next, calculate the volume of the upper cylinder.
Radius of upper cylinder, $r_2 = 8$ cm.
Radius of upper cylinder, $r_2 = 8$ cm.
(Given)
Height of upper cylinder, $h_2 = 60$ cm.
Volume of upper cylinder, $V_2 = \pi r_2^2 h_2$.
Substitute the values from the given information:
$V_2 = \pi (8 \text{ cm})^2 (60 \text{ cm})$.
$V_2 = \pi (64 \times 60)$ cm$^3$.
$V_2 = 3840\pi$ cm$^3$.
... (iii)
The total volume of the iron pole is the sum of the volumes of the two cylinders.
Total Volume, $V_{total} = V_1 + V_2$.
Substitute the values from (ii) and (iii):
$V_{total} = 31680\pi \text{ cm}^3 + 3840\pi \text{ cm}^3$.
$V_{total} = (31680 + 3840)\pi \text{ cm}^3 = 35520\pi \text{ cm}^3$.
... (iv)
Use the given value $\pi = 3.14$ to find the numerical value of the total volume.
$V_{total} = 35520 \times 3.14$ cm$^3$.
$35520 \times 3.14 = 111532.8$ cm$^3$.
Now, calculate the mass of the pole using the given density.
Mass of 1 cm$^3$ of iron $\approx 8$ g.
Total mass = Total Volume $\times$ Density.
Mass $= 111532.8 \text{ cm}^3 \times 8 \text{ g/cm}^3$.
Mass $= 892262.4$ g.
The mass can also be expressed in kilograms (1 kg = 1000 g).
Mass $= \frac{892262.4}{1000}$ kg $= 892.2624$ kg.
Final Answer:
The mass of the pole is approximately $892262.4$ g or $892.2624$ kg.
Question 7. A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
Answer:
Given:
Solid shape: a right circular cone standing on a hemisphere.
Radius of cone, $r_c = 60$ cm.
Height of cone, $h_c = 120$ cm.
Radius of hemisphere, $r_h = 60$ cm.
The solid is placed upright in a right circular cylinder full of water.
Radius of cylinder, $R = 60$ cm.
Height of cylinder, $H = 180$ cm.
The solid touches the bottom of the cylinder.
To Find:
The volume of water left in the cylinder.
Solution:
The solid is a combination of a hemisphere and a cone.
Radius of hemisphere = Radius of cone base = 60 cm. Let $r = 60$ cm.
Radius of solid, $r = 60$ cm.
... (i)
Height of cone, $h_c = 120$ cm.
The volume of the solid is the sum of the volume of the hemisphere and the volume of the cone.
Volume of hemisphere $= \frac{2}{3} \pi r^3$.
Volume of cone $= \frac{1}{3} \pi r^2 h_c$.
Volume of Solid, $V_{solid} = \text{Volume of hemisphere} + \text{Volume of cone}$.
$V_{solid} = \frac{2}{3} \pi r^3 + \frac{1}{3} \pi r^2 h_c$.
Substitute the values of $r$ and $h_c$:
$V_{solid} = \frac{2}{3} \pi (60)^3 + \frac{1}{3} \pi (60)^2 (120)$
$V_{solid} = \frac{2}{3} \pi (216000) + \frac{1}{3} \pi (3600)(120)$
$V_{solid} = 2 \pi (72000) + \pi (1200)(120)$
$V_{solid} = 144000\pi + 144000\pi$
Volume of Solid, $V_{solid} = 288000\pi$ cm$^3$.
... (ii)
The solid is placed in a right circular cylinder full of water.
Radius of cylinder, $R = 60$ cm.
Height of cylinder, $H = 180$ cm.
Note that the radius of the cylinder is equal to the radius of the solid's base ($R=r=60$ cm).
The total height of the solid is the height of the cone plus the radius of the hemisphere: $120 \text{ cm} + 60 \text{ cm} = 180$ cm.
This total height of the solid is equal to the height of the cylinder ($180$ cm).
This confirms the solid fits perfectly inside the cylinder, with its base touching the bottom.
The volume of water that was initially in the cylinder is equal to the volume of the cylinder.
Volume of cylinder, $V_{cylinder} = \pi R^2 H$.
Substitute the values of $R$ and $H$:
$V_{cylinder} = \pi (60)^2 (180)$
$V_{cylinder} = \pi (3600)(180)$
Volume of cylinder, $V_{cylinder} = 648000\pi$ cm$^3$.
... (iii)
When the solid is placed in the cylinder full of water, the volume of water that spills out is equal to the volume of the solid.
The volume of water left in the cylinder is the initial volume of water (volume of cylinder) minus the volume of water that spilled out (volume of solid).
Volume of water left $= V_{cylinder} - V_{solid}$.
Substitute the values from (iii) and (ii):
Volume of water left $= 648000\pi \text{ cm}^3 - 288000\pi \text{ cm}^3$.
Volume of water left $= (648000 - 288000)\pi$ cm$^3$.
Volume of water left $= 360000\pi$ cm$^3$.
Final Answer:
The volume of water left in the cylinder is $360000\pi \text{ cm}^3$.
Question 8. A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm3 . Check whether she is correct, taking the above as the inside measurements, and π= 3.14.
Answer:
Given:
Spherical glass vessel with a cylindrical neck.
For the cylindrical neck:
Length (Height), $h = 8$ cm.
Diameter, $d_c = 2$ cm.
For the spherical part:
Diameter, $d_s = 8.5$ cm.
Child's measured volume = 345 cm$^3$.
Use $\pi = 3.14$.
To Find:
Check if the child's measured volume is correct by calculating the actual volume of the vessel.
Solution:
The vessel consists of a cylindrical neck and a spherical base.
First, calculate the volume of the cylindrical neck.
Diameter of the cylindrical neck, $d_c = 2$ cm.
Radius of the cylindrical neck, $r_c = \frac{d_c}{2} = \frac{2}{2}$ cm.
Radius of cylinder, $r_c = 1$ cm.
... (i)
Height of the cylindrical neck, $h = 8$ cm.
Height of cylinder, $h = 8$ cm.
(Given)
Volume of the cylindrical neck, $V_{cylinder} = \pi r_c^2 h$.
Substitute the values from (i), the given height, and $\pi = 3.14$:
$V_{cylinder} = 3.14 \times (1)^2 \times 8$ cm$^3$.
$V_{cylinder} = 3.14 \times 1 \times 8 = 25.12$ cm$^3$.
Volume of cylinder, $V_{cylinder} = 25.12$ cm$^3$.
... (ii)
Next, calculate the volume of the spherical part.
Diameter of the spherical part, $d_s = 8.5$ cm.
Radius of the spherical part, $r_s = \frac{d_s}{2} = \frac{8.5}{2}$ cm.
Radius of sphere, $r_s = 4.25$ cm.
... (iii)
Volume of the spherical part, $V_{sphere} = \frac{4}{3} \pi r_s^3$.
Substitute the values from (iii) and $\pi = 3.14$:
$V_{sphere} = \frac{4}{3} \times 3.14 \times (4.25)^3$ cm$^3$.
Calculate $(4.25)^3$:
$(4.25)^2 = 4.25 \times 4.25 = 18.0625$.
$(4.25)^3 = 18.0625 \times 4.25 = 76.765625$.
$V_{sphere} = \frac{4}{3} \times 3.14 \times 76.765625$ cm$^3$.
$V_{sphere} = \frac{12.56 \times 76.765625}{3}$ cm$^3$.
$12.56 \times 76.765625 = 963.984375$.
$V_{sphere} = \frac{963.984375}{3} \approx 321.328125$ cm$^3$.
Volume of sphere, $V_{sphere} \approx 321.3281$ cm$^3$.
... (iv)
The total volume of the vessel is the sum of the volumes of the cylindrical neck and the spherical part.
Total Volume, $V_{total} = V_{cylinder} + V_{sphere}$.
Substitute the values from (ii) and (iv):
$V_{total} \approx 25.12 \text{ cm}^3 + 321.3281 \text{ cm}^3$.
$V_{total} \approx 346.4481$ cm$^3$.
The child measured the volume to be 345 cm$^3$.
Comparing the calculated volume ($346.4481$ cm$^3$) with the child's measured volume ($345$ cm$^3$), we see that they are not exactly the same.
The difference is $346.4481 - 345 = 1.4481$ cm$^3$.
Based on the given precise dimensions and the value of $\pi=3.14$, the actual volume of the vessel is approximately 346.45 cm$^3$. The child's measurement of 345 cm$^3$ is close but not exactly correct.
Final Answer:
The calculated volume of the vessel is approximately $346.45 \text{ cm}^3$.
The child's measurement of 345 cm$^3$ is not exactly correct.
Example 8 to 11 (Before Exercise 13.3)
Example 8. A cone of height 24 cm and radius of base 6 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere.
Answer:
Given:
A cone with height $h = 24$ cm and base radius $r_c = 6$ cm.
The cone is reshaped into a sphere.
To Find:
The radius of the sphere ($r_s$).
Solution:
When a solid is reshaped from one form to another, its volume remains constant.
Volume of cone $= \frac{1}{3} \pi r_c^2 h$.
Substitute the given values for the cone:
Volume of cone $= \frac{1}{3} \pi (6 \text{ cm})^2 (24 \text{ cm})$
Volume of cone $= \frac{1}{3} \pi (36)(24)$ cm$^3$
Volume of cone $= \pi (36) \frac{24}{3}$ cm$^3$
Volume of cone $= \pi (36)(8)$ cm$^3$
Volume of cone $= 288\pi$ cm$^3$.
... (i)
Let the radius of the sphere be $r_s$.
Volume of sphere $= \frac{4}{3} \pi r_s^3$.
Volume of sphere $= \frac{4}{3} \pi r_s^3$.
... (ii)
Since the cone is reshaped into a sphere, their volumes are equal.
Volume of sphere = Volume of cone.
(Volumes are equal upon reshaping)
Equating the volumes from (ii) and (i):
$\frac{4}{3} \pi r_s^3 = 288\pi$.
Divide both sides by $\pi$ (since $\pi \neq 0$):
$\frac{4}{3} r_s^3 = 288$.
Multiply both sides by $\frac{3}{4}$ to solve for $r_s^3$:
$r_s^3 = 288 \times \frac{3}{4}$.
$r_s^3 = \frac{288 \times 3}{4}$.
$r_s^3 = \cancel{288}^{72} \times \frac{3}{\cancel{4}_1}$.
$r_s^3 = 72 \times 3$.
$r_s^3 = 216$.
To find $r_s$, we need to find the cube root of 216.
$r_s = \sqrt[3]{216}$.
We know that $6 \times 6 \times 6 = 36 \times 6 = 216$.
So, the cube root of 216 is 6.
Radius of sphere, $r_s = 6$ cm.
... (iii)
The radius of the sphere is 6 cm.
Final Answer:
The radius of the sphere is $6 \text{ cm}$.
Example 9. Selvi’s house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m × 1.44 m × 95cm. The overhead tank has its radius 60 cm and height 95 cm. Find the height of the water left in the sump after the overhead tank has been completely filled with water from the sump which had been full. Compare the capacity of the tank with that of the sump. (Use π = 3.14)
Answer:
Given:
Shed shape: cuboid surmounted by a half cylinder.
Sump shape: cuboid.
Sump dimensions: $1.57 \text{ m} \times 1.44 \text{ m} \times 95 \text{ cm}$.
Overhead tank shape: cylinder.
Overhead tank radius = 60 cm.
Overhead tank height = 95 cm.
Initial state: Sump is full, overhead tank is empty.
Final state: Overhead tank is completely filled from the sump.
Use $\pi = 3.14$.
To Find:
1. The height of the water left in the sump after filling the overhead tank.
2. Compare the capacity of the tank with that of the sump.
Solution:
First, let's ensure all dimensions are in the same unit. We will convert meters to centimeters.
$1 \text{ m} = 100 \text{ cm}$.
Sump dimensions:
Length, $l = 1.57 \text{ m} = 1.57 \times 100 \text{ cm} = 157 \text{ cm}$.
Width, $w = 1.44 \text{ m} = 1.44 \times 100 \text{ cm} = 144 \text{ cm}$.
Initial height of water in sump, $h_{sump, initial} = 95 \text{ cm}$.
Overhead tank dimensions:
Radius, $r = 60 \text{ cm}$.
Height, $h_{tank} = 95 \text{ cm}$.
The volume of water initially in the sump is the volume of the cuboidal sump.
Initial volume of sump, $V_{sump, initial} = l \times w \times h_{sump, initial}$.
$V_{sump, initial} = 157 \text{ cm} \times 144 \text{ cm} \times 95 \text{ cm}$.
$157 \times 144 = 22608$.
$V_{sump, initial} = 22608 \times 95 = 2147760$ cm$^3$.
Initial volume of sump $= 2147760 \text{ cm}^3$.
... (i)
The volume of water needed to fill the overhead tank is the volume of the cylindrical tank.
Volume of tank, $V_{tank} = \pi r^2 h_{tank}$.
Using $\pi = 3.14$:
$V_{tank} = 3.14 \times (60 \text{ cm})^2 \times 95 \text{ cm}$.
$V_{tank} = 3.14 \times 3600 \times 95$ cm$^3$.
$3600 \times 95 = 342000$.
$V_{tank} = 3.14 \times 342000 = 1073880$ cm$^3$.
Volume of tank $= 1073880 \text{ cm}^3$.
... (ii)
When the overhead tank is filled, the volume of water transferred from the sump is equal to the volume of the tank.
The volume of water left in the sump is the initial volume minus the volume transferred.
Volume of water left in sump, $V_{sump, left} = V_{sump, initial} - V_{tank}$.
$V_{sump, left} = 2147760 \text{ cm}^3 - 1073880 \text{ cm}^3$.
Volume of water left in sump $= 1073880 \text{ cm}^3$.
... (iii)
The water left in the sump still forms a cuboid with the same base dimensions ($l$ and $w$) but a reduced height. Let the height of the water left in the sump be $h_{sump, left}$.
$V_{sump, left} = l \times w \times h_{sump, left}$.
We know $l = 157$ cm and $w = 144$ cm.
Base area of sump $= 157 \times 144 = 22608$ cm$^2$.
Substitute the value of $V_{sump, left}$ from (iii):
$1073880 \text{ cm}^3 = 22608 \text{ cm}^2 \times h_{sump, left}$.
To find $h_{sump, left}$, divide the volume by the base area:
$h_{sump, left} = \frac{1073880}{22608}$ cm.
$1073880 \div 22608 = 47.5$.
Height of water left in sump $= 47.5$ cm.
... (iv)
Now, we need to compare the capacity of the tank with that of the sump.
Capacity of tank $= V_{tank} = 1073880$ cm$^3$.
Capacity of sump $= V_{sump, initial} = 2147760$ cm$^3$.
Let's find the ratio of the capacities:
Ratio $= \frac{\text{Capacity of sump}}{\text{Capacity of tank}} = \frac{2147760}{1073880}$.
Ratio $= 2$.
This means the capacity of the sump is twice the capacity of the tank.
Final Answer:
The height of the water left in the sump is $47.5 \text{ cm}$.
The capacity of the sump is twice the capacity of the tank.
Example 10. A copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Answer:
Given:
For the copper rod:
Diameter = 1 cm
Length ($h_{rod}$) = 8 cm
For the copper wire:
Length ($h_{wire}$) = 18 m
To Find:
The thickness (diameter) of the wire.
Solution:
The copper rod is in the shape of a cylinder.
First, calculate the radius of the copper rod:
Radius of rod ($r_{rod}$) = $\frac{\text{Diameter}}{2} = \frac{1}{2}$ cm $= 0.5$ cm.
Calculate the volume of the copper rod using the formula for the volume of a cylinder, $V = \pi r^2 h$:
Volume of rod ($V_{rod}$) = $\pi r_{rod}^2 h_{rod}$
$V_{rod} = \pi (0.5)^2 \times 8$
$V_{rod} = \pi \times 0.25 \times 8$
$V_{rod} = 2\pi$ cm³
The copper wire is also in the shape of a cylinder. Let its radius be $r_{wire}$ cm.
The length of the wire is given in meters, so we need to convert it to centimeters for consistency:
Length of wire ($h_{wire}$) = 18 m
Since 1 m = 100 cm,
$h_{wire} = 18 \times 100$ cm $= 1800$ cm.
Calculate the volume of the copper wire:
Volume of wire ($V_{wire}$) = $\pi r_{wire}^2 h_{wire}$
$V_{wire} = \pi r_{wire}^2 \times 1800$
When the copper rod is drawn into a wire, the volume of the copper remains constant. Therefore, the volume of the rod is equal to the volume of the wire.
Volume of rod = Volume of wire
$V_{rod} = V_{wire}$
$2\pi = \pi r_{wire}^2 \times 1800$
We can cancel $\pi$ from both sides:
$2 = 1800 \times r_{wire}^2$
Now, solve for $r_{wire}^2$:
$r_{wire}^2 = \frac{2}{1800}$
Simplify the fraction:
$r_{wire}^2 = \frac{\cancel{2}^{1}}{\cancel{1800}_{900}}$
$r_{wire}^2 = \frac{1}{900}$
Take the square root of both sides to find the radius of the wire ($r_{wire}$):
$r_{wire} = \sqrt{\frac{1}{900}}$
$r_{wire} = \frac{\sqrt{1}}{\sqrt{900}}$
$r_{wire} = \frac{1}{30}$ cm
The thickness of the wire is its diameter ($d_{wire}$). The diameter is twice the radius.
Thickness ($d_{wire}$) = $2 \times r_{wire}$
$d_{wire} = 2 \times \frac{1}{30}$
$d_{wire} = \frac{2}{30}$
Simplify the fraction:
$d_{wire} = \frac{\cancel{2}^{1}}{\cancel{30}_{15}}$
$d_{wire} = \frac{1}{15}$ cm
The thickness can also be expressed in millimeters (1 cm = 10 mm):
Thickness = $\frac{1}{15} \text{ cm} = \frac{1}{15} \times 10 \text{ mm} = \frac{10}{15} \text{ mm} = \frac{2}{3} \text{ mm}$
$\frac{2}{3} \text{ mm} \approx 0.67 \text{ mm}$
Therefore, the thickness of the wire is $\frac{1}{15}$ cm or approximately 0.67 mm.
Example 11. A hemispherical tank full of water is emptied by a pipe at the rate of $3\frac{4}{7}$ litres per second. How much time will it take to empty half the tank, if it is 3m in diameter? (Take π = $\frac{22}{7}$ )
Answer:
Given:
Shape of the tank: Hemispherical
Diameter of the tank = 3 m
Rate of emptying water = $3\frac{4}{7}$ litres per second
Portion of the tank to be emptied = Half
Value of $\pi = \frac{22}{7}$
To Find:
The time required to empty half the tank.
Solution:
First, find the radius of the hemispherical tank:
Radius (r) = $\frac{\text{Diameter}}{2} = \frac{3}{2}$ m.
Next, calculate the volume of the hemispherical tank using the formula $V = \frac{2}{3}\pi r^3$.
$V = \frac{2}{3} \times \pi \times r^3$
$V = \frac{2}{3} \times \frac{22}{7} \times \left(\frac{3}{2}\right)^3$
$V = \frac{2}{3} \times \frac{22}{7} \times \frac{3}{2} \times \frac{3}{2} \times \frac{3}{2}$
$V = \frac{2}{3} \times \frac{22}{7} \times \frac{27}{8}$
Simplify the expression:
$V = \frac{\cancel{2}}{\cancel{3}} \times \frac{\cancel{22}^{11}}{7} \times \frac{\cancel{27}^{9}}{\cancel{8}_{4}}$
$V = \frac{11 \times 9}{7 \times 4}$
$V = \frac{99}{28}$ m³
This is the volume of the full tank.
We need to find the time to empty half the tank. So, the volume of water to be emptied is:
Volume to empty ($V_{empty}$) = $\frac{1}{2} \times V$
$V_{empty} = \frac{1}{2} \times \frac{99}{28}$ m³
$V_{empty} = \frac{99}{56}$ m³
The rate of emptying is given in litres per second. We need to convert the volume to be emptied from cubic meters (m³) to litres (L).
We know that 1 m³ = 1000 litres.
$V_{empty} = \frac{99}{56} \times 1000$ litres
$V_{empty} = \frac{99000}{56}$ litres
Simplify the fraction by dividing numerator and denominator by their greatest common divisor, which is 8:
$V_{empty} = \frac{99000 \div 8}{56 \div 8} = \frac{12375}{7}$ litres
Now, convert the rate of emptying from a mixed fraction to an improper fraction:
Rate = $3\frac{4}{7} = \frac{(3 \times 7) + 4}{7} = \frac{21 + 4}{7} = \frac{25}{7}$ litres per second.
Finally, calculate the time required to empty half the tank.
Time = $\frac{\text{Volume to be emptied}}{\text{Rate of emptying}}$
Time = $\frac{\frac{12375}{7} \text{ litres}}{\frac{25}{7} \text{ litres/second}}$
Time = $\frac{12375}{7} \times \frac{7}{25}$ seconds
Time = $\frac{12375}{\cancel{7}} \times \frac{\cancel{7}}{25}$ seconds
Time = $\frac{12375}{25}$ seconds
Perform the division:
Time = $495$ seconds
Convert the time from seconds to minutes and seconds.
Since 1 minute = 60 seconds,
Time = $\frac{495}{60}$ minutes
To find the number of minutes and remaining seconds, divide 495 by 60:
$495 \div 60 = 8$ with a remainder of $15$.
$495$ seconds $= 8 \times 60$ seconds $+ 15$ seconds $= 8$ minutes $15$ seconds.
Therefore, it will take 8 minutes and 15 seconds to empty half the tank.
Exercise 13.3
Take π = $\frac{22}{7}$ ,unless stated otherwise.
Question 1. A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Answer:
Given:
For the metallic sphere:
Radius ($r_{sphere}$) = 4.2 cm
For the cylinder:
Radius ($r_{cylinder}$) = 6 cm
To Find:
The height of the cylinder ($h_{cylinder}$).
Solution:
The metallic sphere is melted and recast into a cylinder. This means the volume of the metal remains constant.
Volume of the sphere = Volume of the cylinder
First, calculate the volume of the sphere using the formula $V_{sphere} = \frac{4}{3}\pi r_{sphere}^3$.
$V_{sphere} = \frac{4}{3} \pi (4.2)^3$
$V_{sphere} = \frac{4}{3} \pi (4.2 \times 4.2 \times 4.2)$
$V_{sphere} = \frac{4}{3} \pi (74.088)$ cm³
Next, express the volume of the cylinder using the formula $V_{cylinder} = \pi r_{cylinder}^2 h_{cylinder}$.
$V_{cylinder} = \pi (6)^2 h_{cylinder}$
$V_{cylinder} = \pi \times 36 \times h_{cylinder}$
$V_{cylinder} = 36\pi h_{cylinder}$ cm³
Now, equate the volume of the sphere and the volume of the cylinder:
$V_{sphere} = V_{cylinder}$
$\frac{4}{3} \pi (74.088) = 36\pi h_{cylinder}$
We can cancel $\pi$ from both sides of the equation:
$\frac{4}{3} \times 74.088 = 36 \times h_{cylinder}$
Calculate $\frac{74.088}{3}$:
$\frac{74.088}{3} = 24.696$
So, the equation becomes:
$4 \times 24.696 = 36 \times h_{cylinder}$
$98.784 = 36 \times h_{cylinder}$
Now, solve for $h_{cylinder}$:
$h_{cylinder} = \frac{98.784}{36}$
Performing the division:
$h_{cylinder} = 2.744$ cm
Therefore, the height of the cylinder is 2.744 cm.
Question 2. Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
Answer:
Given:
Three metallic spheres with radii:
Radius of the first sphere ($r_1$) = 6 cm
Radius of the second sphere ($r_2$) = 8 cm
Radius of the third sphere ($r_3$) = 10 cm
These spheres are melted and recast into a single solid sphere.
To Find:
The radius of the resulting single solid sphere (Let it be R).
Solution:
When the three spheres are melted and recast into a single sphere, the total volume of the metal remains constant. Therefore, the volume of the resulting single sphere will be equal to the sum of the volumes of the three individual spheres.
The formula for the volume of a sphere with radius $r$ is $V = \frac{4}{3}\pi r^3$.
Volume of the first sphere ($V_1$) = $\frac{4}{3}\pi r_1^3 = \frac{4}{3}\pi (6)^3$ cm³
Volume of the second sphere ($V_2$) = $\frac{4}{3}\pi r_2^3 = \frac{4}{3}\pi (8)^3$ cm³
Volume of the third sphere ($V_3$) = $\frac{4}{3}\pi r_3^3 = \frac{4}{3}\pi (10)^3$ cm³
Volume of the resulting sphere ($V_{result}$) = $\frac{4}{3}\pi R^3$ cm³
According to the principle of conservation of volume:
$V_{result} = V_1 + V_2 + V_3$
$\frac{4}{3}\pi R^3 = \frac{4}{3}\pi (6)^3 + \frac{4}{3}\pi (8)^3 + \frac{4}{3}\pi (10)^3$
We can factor out the common term $\frac{4}{3}\pi$ from the right side:
$\frac{4}{3}\pi R^3 = \frac{4}{3}\pi (6^3 + 8^3 + 10^3)$
Divide both sides by $\frac{4}{3}\pi$:
$R^3 = 6^3 + 8^3 + 10^3$
Calculate the cubes of the radii:
$6^3 = 6 \times 6 \times 6 = 216$
$8^3 = 8 \times 8 \times 8 = 512$
$10^3 = 10 \times 10 \times 10 = 1000$
Substitute these values back into the equation for $R^3$:
$R^3 = 216 + 512 + 1000$
Perform the addition:
$R^3 = 1728$
To find the radius R, we need to take the cube root of 1728:
$R = \sqrt[3]{1728}$
We can find the cube root by prime factorization or by recognizing common cubes. Let's use prime factorization for 1728:
$\begin{array}{c|cc} 2 & 1728 \\ \hline 2 & 864 \\ \hline 2 & 432 \\ \hline 2 & 216 \\ \hline 2 & 108 \\ \hline 2 & 54 \\ \hline 3 & 27 \\ \hline 3 & 9 \\ \hline 3 & 3 \\ \hline & 1 \end{array}$
$1728 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3 = (2 \times 2 \times 3) \times (2 \times 2 \times 3) \times (2 \times 2 \times 3) = 12 \times 12 \times 12 = 12^3$
So, $R = \sqrt[3]{12^3} = 12$
Therefore, the radius of the resulting sphere is 12 cm.
Question 3. A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Answer:
Given:
For the cylindrical well:
Depth (Height, $h_{well}$) = 20 m
Diameter = 7 m
For the cuboidal platform:
Length (L) = 22 m
Breadth (B) = 14 m
The earth dug from the well is used to form the platform.
To Find:
The height of the platform ($H_{platform}$).
Solution:
The well is in the shape of a cylinder, and the platform is in the shape of a cuboid.
The volume of the earth dug out from the well is equal to the volume of the platform formed.
Volume of earth dug = Volume of the cylindrical well
Volume of platform = Volume of the cuboid
Volume of well = Volume of platform
First, calculate the volume of the cylindrical well.
Radius of the well ($r_{well}$) = $\frac{\text{Diameter}}{2} = \frac{7}{2}$ m.
The formula for the volume of a cylinder is $V = \pi r^2 h$. Let's use $\pi = \frac{22}{7}$.
Volume of well ($V_{well}$) = $\pi r_{well}^2 h_{well}$
$V_{well} = \frac{22}{7} \times \left(\frac{7}{2}\right)^2 \times 20$
$V_{well} = \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 20$
$V_{well} = \frac{22}{\cancel{7}} \times \frac{\cancel{7}}{2} \times \frac{7}{2} \times 20$
Simplify the calculation:
$V_{well} = \frac{\cancel{22}^{11}}{\cancel{2}} \times \frac{7}{\cancel{2}} \times \cancel{20}^{10}$
$V_{well} = 11 \times 7 \times 10$
$V_{well} = 770$ m³
Next, express the volume of the cuboidal platform.
The formula for the volume of a cuboid is $V = L \times B \times H$.
Volume of platform ($V_{platform}$) = $L \times B \times H_{platform}$
$V_{platform} = 22 \times 14 \times H_{platform}$
$V_{platform} = 308 \times H_{platform}$ m³
Now, equate the volume of the well and the volume of the platform:
$V_{well} = V_{platform}$
$770 = 308 \times H_{platform}$
Solve for the height of the platform ($H_{platform}$):
$H_{platform} = \frac{770}{308}$
Simplify the fraction. We can divide both numerator and denominator by common factors. Both are divisible by 77:
$770 \div 77 = 10$
$308 \div 77 = 4$
$H_{platform} = \frac{10}{4}$
Simplify further by dividing by 2:
$H_{platform} = \frac{\cancel{10}^{5}}{\cancel{4}_{2}}$
$H_{platform} = \frac{5}{2}$
$H_{platform} = 2.5$ m
Therefore, the height of the platform is 2.5 m.
Question 4. A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
Answer:
Given:
For the cylindrical well:
Diameter = 3 m
Depth (Height, $h_{well}$) = 14 m
For the circular embankment (hollow cylinder):
Width of the embankment = 4 m
The earth dug from the well is used to form the embankment.
To Find:
The height of the embankment ($H_{embankment}$).
Solution:
The well is in the shape of a cylinder. The earth dug out forms the volume of this cylinder.
Radius of the well ($r_{well}$) = $\frac{\text{Diameter}}{2} = \frac{3}{2}$ m.
Volume of the earth dug out = Volume of the cylindrical well
$V_{well} = \pi r_{well}^2 h_{well}$
Using $\pi = \frac{22}{7}$:
$V_{well} = \frac{22}{7} \times \left(\frac{3}{2}\right)^2 \times 14$
$V_{well} = \frac{22}{7} \times \frac{9}{4} \times 14$
$V_{well} = \frac{22}{\cancel{7}} \times \frac{9}{4} \times \cancel{14}^{2}$
$V_{well} = \frac{22 \times 9 \times 2}{4}$
$V_{well} = \frac{\cancel{22}^{11} \times 9 \times \cancel{2}}{\cancel{4}_{1}}$
$V_{well} = 11 \times 9 = 99$ m³
The embankment is formed in the shape of a circular ring (a hollow cylinder) around the well.
The inner radius of the embankment is the same as the radius of the well.
Inner radius ($r_{inner}$) = $r_{well} = \frac{3}{2}$ m.
The width of the embankment is 4 m.
Outer radius ($r_{outer}$) = Inner radius + Width
$r_{outer} = \frac{3}{2} + 4 = \frac{3}{2} + \frac{8}{2} = \frac{11}{2}$ m.
Let the height of the embankment be $H_{embankment}$.
The volume of the embankment is the volume of the earth spread out.
Volume of embankment ($V_{embankment}$) = Volume of outer cylinder - Volume of inner cylinder
$V_{embankment} = \pi r_{outer}^2 H_{embankment} - \pi r_{inner}^2 H_{embankment}$
$V_{embankment} = \pi H_{embankment} (r_{outer}^2 - r_{inner}^2)$
$V_{embankment} = \frac{22}{7} \times H_{embankment} \times \left[ \left(\frac{11}{2}\right)^2 - \left(\frac{3}{2}\right)^2 \right]$
$V_{embankment} = \frac{22}{7} \times H_{embankment} \times \left[ \frac{121}{4} - \frac{9}{4} \right]$
$V_{embankment} = \frac{22}{7} \times H_{embankment} \times \left[ \frac{121 - 9}{4} \right]$
$V_{embankment} = \frac{22}{7} \times H_{embankment} \times \frac{112}{4}$
$V_{embankment} = \frac{22}{7} \times H_{embankment} \times 28$
$V_{embankment} = \frac{22}{\cancel{7}} \times H_{embankment} \times \cancel{28}^{4}$
$V_{embankment} = 22 \times 4 \times H_{embankment}$
$V_{embankment} = 88 \times H_{embankment}$ m³
The volume of the earth dug out is equal to the volume of the embankment.
$V_{well} = V_{embankment}$
$99 = 88 \times H_{embankment}$
Solve for $H_{embankment}$:
$H_{embankment} = \frac{99}{88}$
Simplify the fraction by dividing the numerator and denominator by their greatest common divisor, which is 11:
$H_{embankment} = \frac{\cancel{99}^{9}}{\cancel{88}_{8}}$
$H_{embankment} = \frac{9}{8}$ m
Convert the fraction to a decimal:
$H_{embankment} = 1.125$ m
Therefore, the height of the embankment is $\frac{9}{8}$ m or 1.125 m.
Question 5. A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Answer:
Given:
For the right circular cylindrical container:
Diameter = 12 cm
Height ($h_{cyl}$) = 15 cm
For the ice cream cone (conical part + hemispherical top):
Diameter of cone/hemisphere = 6 cm
Height of conical part ($h_{cone}$) = 12 cm
The container is full of ice cream.
To Find:
The number of ice cream cones that can be filled.
Solution:
First, calculate the volume of ice cream in the cylindrical container.
Radius of the cylinder ($r_{cyl}$) = $\frac{\text{Diameter}}{2} = \frac{12}{2} = 6$ cm.
Volume of the cylinder ($V_{cyl}$) = $\pi r_{cyl}^2 h_{cyl}$
$V_{cyl} = \pi (6)^2 \times 15$
$V_{cyl} = \pi \times 36 \times 15$
$V_{cyl} = 540\pi$ cm³
Next, calculate the volume of ice cream in one cone. This includes the volume of the conical part and the volume of the hemispherical top.
Radius of the conical part ($r_{cone}$) = $\frac{\text{Diameter}}{2} = \frac{6}{2} = 3$ cm.
Volume of the conical part ($V_{cone}$) = $\frac{1}{3}\pi r_{cone}^2 h_{cone}$
$V_{cone} = \frac{1}{3}\pi (3)^2 \times 12$
$V_{cone} = \frac{1}{3}\pi \times 9 \times 12$
$V_{cone} = \pi \times 3 \times 12$
$V_{cone} = 36\pi$ cm³
Radius of the hemispherical top ($r_{hemi}$) = Radius of the cone = 3 cm.
Volume of the hemispherical top ($V_{hemi}$) = $\frac{2}{3}\pi r_{hemi}^3$
$V_{hemi} = \frac{2}{3}\pi (3)^3$
$V_{hemi} = \frac{2}{3}\pi \times 27$
$V_{hemi} = 2\pi \times 9$
$V_{hemi} = 18\pi$ cm³
Total volume of ice cream in one cone ($V_{total\_cone}$) = $V_{cone} + V_{hemi}$
$V_{total\_cone} = 36\pi + 18\pi$
$V_{total\_cone} = 54\pi$ cm³
Let 'n' be the number of cones that can be filled with ice cream.
The total volume of ice cream in 'n' cones must be equal to the volume of ice cream in the cylindrical container.
$n \times V_{total\_cone} = V_{cyl}$
$n \times 54\pi = 540\pi$
Solve for n:
$n = \frac{540\pi}{54\pi}$
Cancel $\pi$ from the numerator and denominator:
$n = \frac{540}{54}$
$n = 10$
Therefore, 10 such cones can be filled with ice cream.
Question 6. How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?
Answer:
Given:
For each silver coin (shape of a cylinder):
Diameter = 1.75 cm
Thickness (Height, $h_{coin}$) = 2 mm
For the cuboid:
Length (L) = 5.5 cm
Breadth (B) = 10 cm
Height (H) = 3.5 cm
The coins are melted to form the cuboid.
To Find:
The number of silver coins (n) that must be melted.
Solution:
Let 'n' be the number of silver coins required.
The total volume of 'n' silver coins must be equal to the volume of the cuboid formed.
Volume of 'n' coins = Volume of the cuboid
First, calculate the volume of one silver coin. Each coin is a cylinder.
Radius of the coin ($r_{coin}$) = $\frac{\text{Diameter}}{2} = \frac{1.75}{2}$ cm.
Convert thickness (height) from mm to cm: $h_{coin} = 2 \text{ mm} = \frac{2}{10} \text{ cm} = 0.2$ cm.
Volume of one coin ($V_{coin}$) = $\pi r_{coin}^2 h_{coin}$
Using $\pi = \frac{22}{7}$:
$V_{coin} = \frac{22}{7} \times \left(\frac{1.75}{2}\right)^2 \times 0.2$
It might be easier to use fractions: $1.75 = \frac{175}{100} = \frac{7}{4}$. So, $r_{coin} = \frac{7/4}{2} = \frac{7}{8}$ cm.
$h_{coin} = 0.2 = \frac{2}{10} = \frac{1}{5}$ cm.
$V_{coin} = \frac{22}{7} \times \left(\frac{7}{8}\right)^2 \times \frac{1}{5}$
$V_{coin} = \frac{22}{7} \times \frac{49}{64} \times \frac{1}{5}$
$V_{coin} = \frac{22}{\cancel{7}} \times \frac{\cancel{49}^{7}}{64} \times \frac{1}{5}$
$V_{coin} = \frac{22 \times 7}{64 \times 5}$
$V_{coin} = \frac{\cancel{22}^{11} \times 7}{\cancel{64}_{32} \times 5}$
$V_{coin} = \frac{11 \times 7}{32 \times 5} = \frac{77}{160}$ cm³
Next, calculate the volume of the cuboid.
Volume of cuboid ($V_{cuboid}$) = $L \times B \times H$
$V_{cuboid} = 5.5 \times 10 \times 3.5$
$V_{cuboid} = \frac{55}{10} \times 10 \times \frac{35}{10}$
$V_{cuboid} = 55 \times \frac{35}{10}$
$V_{cuboid} = \frac{55 \times 35}{10} = \frac{1925}{10} = 192.5$ cm³
Alternatively, as a fraction: $V_{cuboid} = \frac{1925}{10} = \frac{385}{2}$ cm³
Now, equate the total volume of 'n' coins to the volume of the cuboid:
$n \times V_{coin} = V_{cuboid}$
$n \times \frac{77}{160} = \frac{385}{2}$
Solve for n:
$n = \frac{385}{2} \div \frac{77}{160}$
$n = \frac{385}{2} \times \frac{160}{77}$
Simplify the expression:
$n = \frac{\cancel{385}^{5}}{\cancel{2}_{1}} \times \frac{\cancel{160}^{80}}{\cancel{77}_{1}}$ (Note: $385 \div 77 = 5$ and $160 \div 2 = 80$)
$n = 5 \times 80$
$n = 400$
Therefore, 400 silver coins must be melted to form the cuboid.
Question 7. A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
Answer:
Given:
For the cylindrical bucket:
Height ($h_{cyl}$) = 32 cm
Radius of base ($r_{cyl}$) = 18 cm
For the conical heap:
Height ($h_{cone}$) = 24 cm
The sand from the bucket forms the conical heap.
To Find:
1. The radius of the conical heap ($r_{cone}$)
2. The slant height of the conical heap ($l_{cone}$)
Solution:
The volume of sand in the cylindrical bucket is equal to the volume of sand in the conical heap.
Volume of cylindrical bucket ($V_{cyl}$) = $\pi r_{cyl}^2 h_{cyl}$
$V_{cyl} = \pi (18)^2 \times 32$
$V_{cyl} = \pi \times 324 \times 32$
$V_{cyl} = 10368\pi$ cm³
Volume of conical heap ($V_{cone}$) = $\frac{1}{3}\pi r_{cone}^2 h_{cone}$
$V_{cone} = \frac{1}{3}\pi r_{cone}^2 \times 24$
$V_{cone} = \pi r_{cone}^2 \times \frac{24}{3}$
$V_{cone} = 8\pi r_{cone}^2$ cm³
Equating the volumes:
$V_{cyl} = V_{cone}$
$10368\pi = 8\pi r_{cone}^2$
Divide both sides by $8\pi$:
$r_{cone}^2 = \frac{10368\pi}{8\pi}$
$r_{cone}^2 = \frac{10368}{8}$
$r_{cone}^2 = 1296$
Take the square root of both sides:
$r_{cone} = \sqrt{1296}$
Since $36 \times 36 = 1296$,
$r_{cone} = 36$ cm
So, the radius of the conical heap is 36 cm.
Now, find the slant height ($l_{cone}$) of the conical heap using the formula $l^2 = r^2 + h^2$.
$l_{cone}^2 = r_{cone}^2 + h_{cone}^2$
$l_{cone}^2 = (36)^2 + (24)^2$
$l_{cone}^2 = 1296 + 576$
$l_{cone}^2 = 1872$
Take the square root of both sides:
$l_{cone} = \sqrt{1872}$
To simplify $\sqrt{1872}$, find the prime factorization of 1872:
$1872 = 2 \times 936 = 2 \times 2 \times 468 = 2^2 \times 2 \times 234 = 2^3 \times 2 \times 117 = 2^4 \times (9 \times 13) = 2^4 \times 3^2 \times 13$
$l_{cone} = \sqrt{2^4 \times 3^2 \times 13}$
$l_{cone} = \sqrt{(2^2)^2 \times 3^2 \times 13}$
$l_{cone} = 2^2 \times 3 \times \sqrt{13}$
$l_{cone} = 4 \times 3 \times \sqrt{13}$
$l_{cone} = 12\sqrt{13}$ cm
Therefore, the radius of the conical heap is 36 cm and the slant height of the heap is $12\sqrt{13}$ cm.
Question 8. Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
Answer:
Given:
For the canal (cross-section is a rectangle):
Width (B) = 6 m
Depth (H) = 1.5 m
Speed of water flow = 10 km/h
Time duration (t) = 30 minutes
Required height of standing water in the field ($h_{field}$) = 8 cm
To Find:
The area that will be irrigated in 30 minutes.
Solution:
First, let's convert the speed and time to consistent units (meters and hours).
Speed of water = 10 km/h = $10 \times 1000$ m/h = 10000 m/h.
Time duration = 30 minutes = $\frac{30}{60}$ hours = 0.5 hours.
The length of the water column that flows through the canal in 30 minutes can be calculated as:
Length (L) = Speed × Time
L = 10000 m/h × 0.5 h = 5000 m.
The volume of water flowing out of the canal in 30 minutes is the volume of a cuboid with length L, width B, and depth H.
Volume of water from canal ($V_{canal}$) = L × B × H
$V_{canal} = 5000 \text{ m} \times 6 \text{ m} \times 1.5 \text{ m}$
$V_{canal} = 5000 \times 9$ m³
$V_{canal} = 45000$ m³
This volume of water is used to irrigate a certain area, creating a standing water height of 8 cm.
Convert the required standing water height to meters:
$h_{field} = 8 \text{ cm} = \frac{8}{100} \text{ m} = 0.08$ m.
Let the area irrigated be A (in m²).
The volume of water used for irrigation ($V_{field}$) is the area multiplied by the height of standing water.
$V_{field} = \text{Area} \times h_{field}$
$V_{field} = A \times 0.08$ m³
The volume of water from the canal is equal to the volume of water used for irrigation.
$V_{canal} = V_{field}$
$45000 = A \times 0.08$
Solve for Area (A):
$A = \frac{45000}{0.08}$
$A = \frac{45000}{8/100}$
$A = 45000 \times \frac{100}{8}$
$A = \frac{4500000}{8}$
$A = 562500$ m²
The area can also be expressed in hectares.
Since 1 hectare = 10000 m²,
Area = $\frac{562500}{10000}$ hectares
Area = 56.25 hectares
Therefore, the area that will be irrigated in 30 minutes is 562,500 m² or 56.25 hectares.
Question 9. A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
Answer:
Given:
For the connecting pipe (cylindrical):
Internal diameter = 20 cm
Rate of water flow = 3 km/h
For the cylindrical tank:
Diameter = 10 m
Depth (Height, $h_{tank}$) = 2 m
To Find:
The time required to fill the tank.
Solution:
First, let's establish consistent units. We will use meters and hours.
Pipe dimensions and flow rate:
Internal diameter of pipe = 20 cm = $\frac{20}{100}$ m = 0.2 m.
Internal radius of pipe ($r_{pipe}$) = $\frac{\text{Diameter}}{2} = \frac{0.2}{2}$ m = 0.1 m.
Speed of water flow = 3 km/h = $3 \times 1000$ m/h = 3000 m/h.
This speed represents the length of the water column flowing through the pipe in one hour.
Volume of water flowing through the pipe per hour = (Cross-sectional area of pipe) × (Speed of water)
Cross-sectional area of pipe = $\pi r_{pipe}^2 = \pi (0.1)^2 = 0.01\pi$ m².
Rate of flow (Volume per hour) = $0.01\pi \text{ m}^2 \times 3000 \text{ m/h} = 30\pi$ m³/h.
Tank dimensions and volume:
Diameter of tank = 10 m.
Radius of tank ($r_{tank}$) = $\frac{10}{2}$ m = 5 m.
Height (depth) of tank ($h_{tank}$) = 2 m.
Volume of the cylindrical tank ($V_{tank}$) = $\pi r_{tank}^2 h_{tank}$
$V_{tank} = \pi (5)^2 \times 2$
$V_{tank} = \pi \times 25 \times 2$
$V_{tank} = 50\pi$ m³
Time calculation:
Let 't' be the time in hours required to fill the tank.
The total volume of water that flows into the tank in time 't' must be equal to the volume of the tank.
Volume of water flowed = Rate of flow × Time
$V_{tank}$ = (Volume per hour) × t
$50\pi = 30\pi \times t$
Solve for t:
$t = \frac{50\pi}{30\pi}$ hours
Cancel $\pi$ from numerator and denominator:
$t = \frac{50}{30}$ hours
$t = \frac{5}{3}$ hours
Convert the time from hours to minutes.
Since 1 hour = 60 minutes,
$t = \frac{5}{3} \times 60$ minutes
$t = 5 \times \frac{60}{3}$ minutes
$t = 5 \times 20$ minutes
$t = 100$ minutes
Therefore, it will take 100 minutes (or 1 hour and 40 minutes) to fill the tank.
Example 12 to 14 (Before Exercise 13.4)
Example 12. The radii of the ends of a frustum of a cone 45 cm high are 28 cm and 7 cm (see Fig. 13.21). Find its volume, the curved surface area and the total suface area (Take π = $\frac{22}{7}$ )
Answer:
Given:
A frustum of a cone.
Height of the frustum ($h$) = 45 cm.
Radius of the larger circular end ($R$) = 28 cm.
Radius of the smaller circular end ($r$) = 7 cm.
Value of $\pi = \frac{22}{7}$.
To Find:
1. Volume of the frustum ($V$).
2. Curved Surface Area (CSA) of the frustum.
3. Total Surface Area (TSA) of the frustum.
Solution:
1. Volume of the Frustum:
The formula for the volume of a frustum of a cone is:
$V = \frac{1}{3}\pi h (R^2 + r^2 + Rr)$
Substitute the given values:
$V = \frac{1}{3} \times \frac{22}{7} \times 45 \times (28^2 + 7^2 + 28 \times 7)$
Calculate the terms inside the parenthesis:
$28^2 = 784$
$7^2 = 49$
$28 \times 7 = 196$
$R^2 + r^2 + Rr = 784 + 49 + 196 = 1029$
Now substitute this back into the volume formula:
$V = \frac{1}{3} \times \frac{22}{7} \times 45 \times 1029$
Simplify the expression:
$V = \frac{1}{\cancel{3}} \times \frac{22}{\cancel{7}} \times \cancel{45}^{15} \times \cancel{1029}^{147}$
$V = 22 \times 15 \times 147$
$V = 330 \times 147$
$V = 48510$ cm³
So, the volume of the frustum is 48510 cm³.
2. Curved Surface Area (CSA) of the Frustum:
First, we need to find the slant height ($l$) of the frustum. The formula is:
$l = \sqrt{h^2 + (R-r)^2}$
$l = \sqrt{45^2 + (28-7)^2}$
$l = \sqrt{45^2 + 21^2}$
$l = \sqrt{2025 + 441}$
$l = \sqrt{2466}$ cm
The formula for the Curved Surface Area (CSA) of a frustum is:
$\text{CSA} = \pi l (R + r)$
Substitute the values:
$\text{CSA} = \frac{22}{7} \times \sqrt{2466} \times (28 + 7)$
$\text{CSA} = \frac{22}{7} \times \sqrt{2466} \times 35$
$\text{CSA} = 22 \times \sqrt{2466} \times \frac{35}{7}$
$\text{CSA} = 22 \times \sqrt{2466} \times 5$
$\text{CSA} = 110\sqrt{2466}$ cm²
So, the Curved Surface Area of the frustum is $110\sqrt{2466}$ cm².
(Note: $\sqrt{2466} \approx 49.659$. If an approximate value is needed, CSA $\approx 110 \times 49.659 \approx 5462.5$ cm².)
3. Total Surface Area (TSA) of the Frustum:
The Total Surface Area (TSA) is the sum of the CSA and the areas of the two circular ends.
Area of the top circular end (smaller base) = $\pi r^2$
Area$_{top} = \frac{22}{7} \times (7)^2 = \frac{22}{7} \times 49 = 22 \times 7 = 154$ cm²
Area of the bottom circular end (larger base) = $\pi R^2$
Area$_{bottom} = \frac{22}{7} \times (28)^2 = \frac{22}{7} \times 784 = 22 \times 112 = 2464$ cm²
The formula for TSA is:
$\text{TSA} = \text{CSA} + \text{Area}_{top} + \text{Area}_{bottom}$
$\text{TSA} = 110\sqrt{2466} + 154 + 2464$
$\text{TSA} = 110\sqrt{2466} + 2618$ cm²
So, the Total Surface Area of the frustum is $(110\sqrt{2466} + 2618)$ cm².
(Note: Using the approximation CSA $\approx 5462.5$ cm², TSA $\approx 5462.5 + 2618 = 8080.5$ cm².)
Example 13. Hanumappa and his wife Gangamma are busy making jaggery out of sugarcane juice. They have processed the sugarcane juice to make the molasses, which is poured into moulds in the shape of a frustum of a cone having the diameters of its two circular faces as 30 cm and 35 cm and the vertical height of the mould is 14 cm (see Fig. 13.22). If each cm3 of molasses has mass about 1.2 g, find the mass of the molasses that can be poured into each mould.(Take π = $\frac{22}{7}$ )
Answer:
Given:
Shape of the mould: Frustum of a cone.
Diameter of the larger circular face = 35 cm.
Diameter of the smaller circular face = 30 cm.
Vertical height of the mould ($h$) = 14 cm.
Density of molasses = 1.2 g/cm³.
Value of $\pi = \frac{22}{7}$.
To Find:
The mass of the molasses that can be poured into each mould.
Solution:
First, find the radii of the two circular faces of the frustum:
Radius of the larger face ($R$) = $\frac{\text{Diameter}}{2} = \frac{35}{2}$ cm = 17.5 cm.
Radius of the smaller face ($r$) = $\frac{\text{Diameter}}{2} = \frac{30}{2}$ cm = 15 cm.
Next, calculate the volume of the frustum-shaped mould using the formula:
$V = \frac{1}{3}\pi h (R^2 + r^2 + Rr)$
Substitute the given values:
$V = \frac{1}{3} \times \frac{22}{7} \times 14 \times ((17.5)^2 + (15)^2 + (17.5 \times 15))$
Calculate the terms inside the parenthesis:
$(17.5)^2 = 306.25$
$(15)^2 = 225$
$17.5 \times 15 = 262.5$
$R^2 + r^2 + Rr = 306.25 + 225 + 262.5 = 793.75$
Now substitute this back into the volume formula:
$V = \frac{1}{3} \times \frac{22}{7} \times 14 \times 793.75$
Simplify the expression:
$V = \frac{1}{3} \times 22 \times (\frac{14}{7}) \times 793.75$
$V = \frac{1}{3} \times 22 \times 2 \times 793.75$
$V = \frac{44}{3} \times 793.75$
$V = \frac{44}{3} \times \frac{79375}{100}$
$V = \frac{\cancel{44}^{11}}{3} \times \frac{79375}{\cancel{100}_{25}}$
$V = \frac{11}{3} \times \frac{79375}{25}$
$V = \frac{11}{3} \times 3175$
$V = \frac{34925}{3}$ cm³
As a decimal, $V \approx 11641.67$ cm³
Now, find the mass of the molasses that can be poured into the mould.
Mass = Volume × Density
Mass = $V \times 1.2$ g
Mass = $\frac{34925}{3} \times 1.2$ g
Mass = $\frac{34925}{3} \times \frac{12}{10}$ g
Mass = $\frac{34925}{\cancel{3}} \times \frac{\cancel{12}^4}{10}$ g
Mass = $\frac{34925 \times 4}{10}$ g
Mass = $\frac{139700}{10}$ g
Mass = $13970$ g
The mass can also be expressed in kilograms.
Since 1 kg = 1000 g,
Mass = $\frac{13970}{1000}$ kg = 13.97 kg.
Therefore, the mass of the molasses that can be poured into each mould is 13970 g or 13.97 kg (approximately).
Example 14. An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet (see Fig. 13.23). The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket, where we do not take into account the handle of the bucket. Also, find the volume of water the bucket can hold (Take π = $\frac{22}{7}$ )

Answer:
Given:
The bucket consists of a frustum of a cone mounted on a hollow cylindrical base.
Diameter of the top circular end of the frustum = 45 cm.
Diameter of the bottom circular end of the frustum (and the cylinder) = 25 cm.
Total vertical height of the bucket = 40 cm.
Height of the cylindrical base ($h_{cyl}$) = 6 cm.
The bucket is open at the top.
Value of $\pi = \frac{22}{7}$.
To Find:
1. The area of the metallic sheet used to make the bucket (excluding the handle).
2. The volume of water the bucket can hold.
Solution:
First, determine the dimensions (radii and heights) for the frustum and cylindrical parts.
Radius of the top end of the frustum ($R$) = $\frac{45}{2} = 22.5$ cm.
Radius of the bottom end of the frustum ($r$) = $\frac{25}{2} = 12.5$ cm.
Radius of the cylindrical base ($r_{cyl}$) = $r = 12.5$ cm.
Height of the frustum ($h_{frustum}$) = Total height - Height of cylinder = $40 - 6 = 34$ cm.
Height of the cylinder ($h_{cyl}$) = 6 cm.
1. Area of the Metallic Sheet:
The area of the metallic sheet used is the sum of:
(i) Curved Surface Area (CSA) of the frustum.
(ii) Area of the circular base (bottom of frustum / top of cylinder).
(iii) Curved Surface Area (CSA) of the cylindrical base.
(i) CSA of the Frustum:
First, calculate the slant height ($l$) of the frustum:
$l = \sqrt{h_{frustum}^2 + (R-r)^2}$
$l = \sqrt{34^2 + (22.5 - 12.5)^2}$
$l = \sqrt{34^2 + 10^2}$
$l = \sqrt{1156 + 100} = \sqrt{1256}$ cm.
Now, calculate the CSA of the frustum:
$\text{CSA}_{frustum} = \pi l (R + r)$
$\text{CSA}_{frustum} = \frac{22}{7} \times \sqrt{1256} \times (22.5 + 12.5)$
$\text{CSA}_{frustum} = \frac{22}{7} \times \sqrt{1256} \times 35$
$\text{CSA}_{frustum} = 22 \times \sqrt{1256} \times \frac{35}{7} = 22 \times \sqrt{1256} \times 5$
$\text{CSA}_{frustum} = 110\sqrt{1256}$ cm²
(ii) Area of the Circular Base:
$\text{Area}_{base} = \pi r^2$
$\text{Area}_{base} = \frac{22}{7} \times (12.5)^2$
$\text{Area}_{base} = \frac{22}{7} \times 156.25 = \frac{3437.5}{7}$ cm²
(iii) CSA of the Cylindrical Base:
$\text{CSA}_{cyl} = 2 \pi r h_{cyl}$
$\text{CSA}_{cyl} = 2 \times \frac{22}{7} \times 12.5 \times 6$
$\text{CSA}_{cyl} = \frac{44}{7} \times 75 = \frac{3300}{7}$ cm²
Total Area of Sheet:
Total Area = $\text{CSA}_{frustum} + \text{Area}_{base} + \text{CSA}_{cyl}$
Total Area = $110\sqrt{1256} + \frac{3437.5}{7} + \frac{3300}{7}$
Total Area = $110\sqrt{1256} + \frac{3437.5 + 3300}{7}$
Total Area = $110\sqrt{1256} + \frac{6737.5}{7}$ cm²
Using the approximation $\sqrt{1256} \approx 35.44$ cm:
Total Area $\approx 110 \times 35.44 + \frac{6737.5}{7}$
Total Area $\approx 3898.4 + 962.5$
Total Area $\approx 4860.9$ cm²
The area of the metallic sheet used is $(110\sqrt{1256} + \frac{6737.5}{7})$ cm², or approximately 4860.9 cm².
2. Volume of Water the Bucket Can Hold:
The volume of water the bucket can hold is the volume of the frustum part.
$V_{frustum} = \frac{1}{3}\pi h_{frustum} (R^2 + r^2 + Rr)$
$V_{frustum} = \frac{1}{3} \times \frac{22}{7} \times 34 \times ((22.5)^2 + (12.5)^2 + (22.5 \times 12.5))$
$V_{frustum} = \frac{1}{3} \times \frac{22}{7} \times 34 \times (506.25 + 156.25 + 281.25)$
$V_{frustum} = \frac{1}{3} \times \frac{22}{7} \times 34 \times (943.75)$
$V_{frustum} = \frac{22 \times 34 \times 943.75}{21}$
$V_{frustum} = \frac{748 \times 943.75}{21} = \frac{705925}{21}$ cm³
$V_{frustum} \approx 33615.48$ cm³
To express the volume in litres (1 L = 1000 cm³):
Volume in litres = $\frac{33615.48}{1000} \approx 33.615$ L
The volume of water the bucket can hold is $\frac{705925}{21}$ cm³, or approximately 33.62 litres.
Exercise 13.4
Use π = $\frac{22}{7}$ unless stated otherwise.
Question 1. A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
Answer:
Given:
The drinking glass is in the shape of a frustum of a cone.
Height of the frustum ($h$) = 14 cm.
Diameter of the larger circular end ($D_1$) = 4 cm.
Diameter of the smaller circular end ($D_2$) = 2 cm.
To Find:
The capacity (volume) of the glass.
Solution:
First, find the radii of the two circular ends of the frustum:
Radius of the larger end ($R$) = $\frac{D_1}{2} = \frac{4}{2} = 2$ cm.
Radius of the smaller end ($r$) = $\frac{D_2}{2} = \frac{2}{2} = 1$ cm.
The capacity of the glass is the volume of the frustum. The formula for the volume of a frustum of a cone is:
$V = \frac{1}{3}\pi h (R^2 + r^2 + Rr)$
Substitute the given values. We will use $\pi = \frac{22}{7}$.
$V = \frac{1}{3} \times \frac{22}{7} \times 14 \times (2^2 + 1^2 + (2 \times 1))$
Calculate the terms inside the parenthesis:
$2^2 = 4$
$1^2 = 1$
$2 \times 1 = 2$
$R^2 + r^2 + Rr = 4 + 1 + 2 = 7$
Now substitute this back into the volume formula:
$V = \frac{1}{3} \times \frac{22}{7} \times 14 \times 7$
Simplify the expression:
$V = \frac{1}{3} \times \frac{22}{\cancel{7}} \times 14 \times \cancel{7}$
$V = \frac{1}{3} \times 22 \times 14$
$V = \frac{308}{3}$ cm³
The capacity can be expressed as a mixed fraction or a decimal:
$V = 102 \frac{2}{3}$ cm³
Or,
$V \approx 102.67$ cm³
Therefore, the capacity of the glass is $\frac{308}{3}$ cm³ or approximately 102.67 cm³.
Question 2. The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Answer:
Given:
A frustum of a cone.
Slant height ($l$) = 4 cm.
Perimeter (circumference) of the larger circular end ($C_1$) = 18 cm.
Perimeter (circumference) of the smaller circular end ($C_2$) = 6 cm.
To Find:
The Curved Surface Area (CSA) of the frustum.
Solution:
Let $R$ and $r$ be the radii of the larger and smaller circular ends, respectively.
We know that the circumference of a circle is given by $C = 2\pi \times \text{radius}$.
So, $C_1 = 2\pi R = 18$ cm
And $C_2 = 2\pi r = 6$ cm
The formula for the Curved Surface Area (CSA) of a frustum of a cone is given by:
$\text{CSA} = \pi l (R + r)$
We can rewrite this formula using the circumferences. Multiply and divide by 2:
$\text{CSA} = \frac{l}{2} (2\pi R + 2\pi r)$
Substitute the given circumferences $C_1 = 2\pi R$ and $C_2 = 2\pi r$:
$\text{CSA} = \frac{l}{2} (C_1 + C_2)$
Now, substitute the given values for $l$, $C_1$, and $C_2$ into this formula:
$\text{CSA} = \frac{4}{2} (18 + 6)$
$\text{CSA} = 2 \times (24)$
$\text{CSA} = 48$ cm²
Therefore, the curved surface area of the frustum is 48 cm².
Question 3. A fez, the cap used by the Turks, is shaped like the frustum of a cone (see Fig. 13.24). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it.

Answer:
Given:
The fez is shaped like a frustum of a cone.
Radius of the open side (larger base, R) = 10 cm.
Radius of the upper base (closed side, r) = 4 cm.
Slant height ($l$) = 15 cm.
To Find:
The area of the material used for making the fez.
Solution:
The fez is open at the bottom (larger base) and closed at the top (smaller base).
The area of the material used will be the sum of the Curved Surface Area (CSA) of the frustum and the area of the top circular base.
Area of material = CSA of frustum + Area of upper circular base
First, calculate the Curved Surface Area (CSA) of the frustum.
The formula for CSA of a frustum is $\pi l (R + r)$.
Using $\pi = \frac{22}{7}$:
CSA = $\frac{22}{7} \times 15 \times (10 + 4)$
CSA = $\frac{22}{7} \times 15 \times 14$
CSA = $22 \times 15 \times \frac{14}{7}$
CSA = $22 \times 15 \times 2$
CSA = $22 \times 30$
CSA = $660$ cm²
Next, calculate the area of the upper circular base (closed top).
The formula for the area of a circle is $\pi r^2$.
Area$_{top}$ = $\pi r^2$
Area$_{top}$ = $\frac{22}{7} \times (4)^2$
Area$_{top}$ = $\frac{22}{7} \times 16$
Area$_{top}$ = $\frac{352}{7}$ cm²
Now, calculate the total area of the material used.
Total Area = CSA + Area$_{top}$
Total Area = $660 + \frac{352}{7}$
To add these, find a common denominator:
Total Area = $\frac{660 \times 7}{7} + \frac{352}{7}$
Total Area = $\frac{4620}{7} + \frac{352}{7}$
Total Area = $\frac{4620 + 352}{7}$
Total Area = $\frac{4972}{7}$ cm²
The area can also be expressed as a mixed fraction:
$\frac{4972}{7} = 710 \frac{2}{7}$ cm²
Therefore, the area of the material used for making the fez is $\frac{4972}{7}$ cm² or $710 \frac{2}{7}$ cm².
Question 4. A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of ₹ 20 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹ 8 per 100 cm2 . (Take π = 3.14)
Answer:
Given:
The container is in the shape of a frustum of a cone, open at the top.
Height of the frustum ($h$) = 16 cm.
Radius of the upper end (open end, R) = 20 cm.
Radius of the lower end (closed base, r) = 8 cm.
Cost of milk =
Cost of metal sheet =
Value of $\pi = 3.14$.
To Find:
1. Cost of the milk to completely fill the container.
2. Cost of the metal sheet used to make the container.
Solution:
Part 1: Cost of Milk
First, find the capacity (volume) of the container (frustum).
The formula for the volume of a frustum of a cone is:
$V = \frac{1}{3}\pi h (R^2 + r^2 + Rr)$
Substitute the given values:
$V = \frac{1}{3} \times 3.14 \times 16 \times (20^2 + 8^2 + (20 \times 8))$
$V = \frac{1}{3} \times 3.14 \times 16 \times (400 + 64 + 160)$
$V = \frac{1}{3} \times 3.14 \times 16 \times (624)$
$V = 3.14 \times 16 \times (\frac{624}{3})$
$V = 3.14 \times 16 \times 208$
$V = 3.14 \times 3328$
$V = 10449.92$ cm³
Now, convert the volume from cm³ to litres (since 1 litre = 1000 cm³):
Volume in litres = $\frac{10449.92}{1000} = 10.44992$ litres
Calculate the cost of the milk:
Cost of milk = Volume in litres × Rate per litre
Cost of milk = $10.44992 \times 20$
Cost of milk =
Rounding to two decimal places, the cost of milk is
Part 2: Cost of Metal Sheet
The area of the metal sheet used includes the Curved Surface Area (CSA) of the frustum and the area of the lower circular base (since the container is open at the top).
Area of sheet = CSA of frustum + Area of lower base
First, calculate the slant height ($l$) of the frustum:
$l = \sqrt{h^2 + (R-r)^2}$
$l = \sqrt{16^2 + (20-8)^2}$
$l = \sqrt{16^2 + 12^2}$
$l = \sqrt{256 + 144} = \sqrt{400}$
$l = 20$ cm
Next, calculate the CSA of the frustum:
CSA = $\pi l (R + r)$
CSA = $3.14 \times 20 \times (20 + 8)$
CSA = $3.14 \times 20 \times 28$
CSA = $3.14 \times 560$
CSA = $1758.4$ cm²
Now, calculate the area of the lower circular base:
Area$_{base}$ = $\pi r^2$
Area$_{base}$ = $3.14 \times (8)^2$
Area$_{base}$ = $3.14 \times 64$
Area$_{base}$ = $200.96$ cm²
Calculate the total area of the metal sheet:
Total Area = CSA + Area$_{base}$
Total Area = $1758.4 + 200.96$
Total Area = $1959.36$ cm²
Finally, calculate the cost of the metal sheet:
Cost of sheet = $\frac{\text{Total Area}}{100} \times \text{Rate per 100 cm}^2$
Cost of sheet = $\frac{1959.36}{100} \times 8$
Cost of sheet = $19.5936 \times 8$
Cost of sheet =
Rounding to two decimal places, the cost of the metal sheet is
Summary:
The cost of the milk which can completely fill the container is
The cost of the metal sheet used to make the container is
Question 5. A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter $\frac{1}{16}$ cm, find the length of the wire.
Answer:
Given:
A metallic right circular cone:
Total height ($H$) = 20 cm.
Vertical angle = 60°, which means the semi-vertical angle ($\theta$) = $\frac{60^\circ}{2} = 30^\circ$.
The cone is cut at the middle of its height (at height = $\frac{20}{2} = 10$ cm from the top) by a plane parallel to the base, forming a frustum.
The resulting frustum is drawn into a wire (cylindrical shape).
Diameter of the wire = $\frac{1}{16}$ cm.
To Find:
The length of the wire.
Solution:
Let the original cone be ABC, with vertex A and base BC. Let O be the center of the base and V be the vertex. Then $VO = H = 20$ cm. Let $R$ be the radius of the base (OC).
In the right triangle VOC, $\angle VOC = 90^\circ$ and $\angle OVC = \theta = 30^\circ$.
$\tan(\theta) = \frac{OC}{VO} = \frac{R}{H}$
$R = H \tan(30^\circ) = 20 \times \frac{1}{\sqrt{3}} = \frac{20}{\sqrt{3}}$ cm.
The cone is cut at the middle of its height. Let the plane cut the cone at height $h' = 10$ cm from the vertex V. Let the radius of the circular cross-section at this height be $r$.
Consider the smaller cone formed at the top with height $h' = 10$ cm. The semi-vertical angle remains $30^\circ$.
Using trigonometry for the smaller cone:
$r = h' \tan(30^\circ) = 10 \times \frac{1}{\sqrt{3}} = \frac{10}{\sqrt{3}}$ cm.
The frustum obtained has:
Height ($h_{frustum}$) = Height of original cone - Height of smaller cone = $H - h' = 20 - 10 = 10$ cm.
Radius of the larger base ($R$) = $\frac{20}{\sqrt{3}}$ cm.
Radius of the smaller base ($r$) = $\frac{10}{\sqrt{3}}$ cm.
Now, calculate the volume of the frustum:
$V_{frustum} = \frac{1}{3}\pi h_{frustum} (R^2 + r^2 + Rr)$
$V_{frustum} = \frac{1}{3}\pi (10) \left[ \left(\frac{20}{\sqrt{3}}\right)^2 + \left(\frac{10}{\sqrt{3}}\right)^2 + \left(\frac{20}{\sqrt{3}} \times \frac{10}{\sqrt{3}}\right) \right]$
$V_{frustum} = \frac{10\pi}{3} \left[ \frac{400}{3} + \frac{100}{3} + \frac{200}{3} \right]$
$V_{frustum} = \frac{10\pi}{3} \left[ \frac{400 + 100 + 200}{3} \right]$
$V_{frustum} = \frac{10\pi}{3} \left[ \frac{700}{3} \right]$
$V_{frustum} = \frac{7000\pi}{9}$ cm³
This frustum is drawn into a wire of diameter $\frac{1}{16}$ cm.
Radius of the wire ($r_{wire}$) = $\frac{\text{Diameter}}{2} = \frac{1/16}{2} = \frac{1}{32}$ cm.
Let the length of the wire be $L_{wire}$. The wire is a cylinder.
Volume of the wire ($V_{wire}$) = $\pi r_{wire}^2 L_{wire}$
$V_{wire} = \pi \left(\frac{1}{32}\right)^2 L_{wire}$
$V_{wire} = \pi \left(\frac{1}{1024}\right) L_{wire}$
The volume of the metal remains constant during the transformation from frustum to wire.
$V_{frustum} = V_{wire}$
$\frac{7000\pi}{9} = \pi \frac{1}{1024} L_{wire}$
Cancel $\pi$ from both sides:
$\frac{7000}{9} = \frac{1}{1024} L_{wire}$
Solve for $L_{wire}$:
$L_{wire} = \frac{7000}{9} \times 1024$
$L_{wire} = \frac{7168000}{9}$ cm
Calculate the approximate value:
$L_{wire} \approx 796444.44$ cm
Convert the length to meters (1 m = 100 cm):
$L_{wire} = \frac{796444.44}{100} \approx 7964.44$ m
Therefore, the length of the wire is $\frac{7168000}{9}$ cm or approximately 7964.44 m.
Exercise 13.5 (Optional)
Question 1. A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3 .
Answer:
Given:
For the copper wire:
Diameter = 3 mm
Density of copper = 8.88 g/cm³
For the cylinder:
Length (Height, $h_{cyl}$) = 12 cm
Diameter = 10 cm
The wire is wound to cover the curved surface of the cylinder.
To Find:
1. The length of the copper wire ($L_{wire}$).
2. The mass of the copper wire.
Solution:
First, ensure all dimensions are in the same unit (cm).
Diameter of the wire = 3 mm = $\frac{3}{10}$ cm = 0.3 cm.
Diameter of the cylinder = 10 cm.
Radius of the cylinder ($r_{cyl}$) = $\frac{\text{Diameter}}{2} = \frac{10}{2} = 5$ cm.
The wire is wound around the cylinder. Each turn of the wire covers a portion of the cylinder's height equal to the diameter of the wire.
Number of turns required to cover the cylinder's height = $\frac{\text{Height of cylinder}}{\text{Diameter of wire}}$
Number of turns = $\frac{12 \text{ cm}}{0.3 \text{ cm}} = \frac{120}{3} = 40$ turns.
The length of the wire in one turn is equal to the circumference of the base of the cylinder.
Length per turn = $2 \pi r_{cyl}$
Length per turn = $2 \pi (5)$ cm $= 10\pi$ cm.
Total length of the wire ($L_{wire}$) = Number of turns × Length per turn
$L_{wire} = 40 \times 10\pi$
$L_{wire} = 400\pi$ cm
Using $\pi \approx 3.14$:
$L_{wire} \approx 400 \times 3.14 = 1256$ cm.
The length of the wire is 1256 cm (or 12.56 m).
Now, find the mass of the wire. First, calculate the volume of the wire. The wire itself is a cylinder.
Radius of the wire ($r_{wire}$) = $\frac{\text{Diameter of wire}}{2} = \frac{0.3}{2} = 0.15$ cm.
Volume of the wire ($V_{wire}$) = $\pi r_{wire}^2 L_{wire}$
$V_{wire} = \pi (0.15)^2 \times (400\pi)$
$V_{wire} = \pi \times 0.0225 \times 400\pi$
$V_{wire} = 0.0225 \times 400 \times \pi^2$
$V_{wire} = 9\pi^2$ cm³
Using $\pi \approx 3.14$:
$V_{wire} \approx 9 \times (3.14)^2 = 9 \times 9.8596$
$V_{wire} \approx 88.7364$ cm³
Finally, calculate the mass of the wire:
Mass = Volume × Density
Mass = $V_{wire} \times 8.88$ g
Mass $\approx 88.7364 \times 8.88$ g
Mass $\approx 787.979$ g
Rounding to a reasonable number of decimal places, the mass is approximately 787.98 g.
Therefore:
The length of the wire is $400\pi$ cm (approximately 1256 cm or 12.56 m).
The mass of the wire is approximately 787.98 g.
Question 2. A right triangle, whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate.)
Answer:
Given:
A right-angled triangle, let's call it ABC, right-angled at B.
Sides containing the right angle: AB = 3 cm and BC = 4 cm.
The triangle is revolved about its hypotenuse AC.
To Find:
1. The volume of the double cone formed.
2. The surface area of the double cone formed.
Solution:
Step 1: Find the hypotenuse AC.
Using the Pythagorean theorem in $\triangle ABC$:
$AC^2 = AB^2 + BC^2$
$AC^2 = 3^2 + 4^2 = 9 + 16 = 25$
$AC = \sqrt{25} = 5$ cm.
Step 2: Visualize the double cone and find the radius.
When the triangle revolves around the hypotenuse AC, it forms a double cone. The vertex B traces out a circle which forms the common base of the two cones. The radius of this base is the length of the altitude BD drawn from B to AC.
We can find the length of BD (let it be $r$) using the area of $\triangle ABC$.
Area($\triangle ABC$) = $\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times AB \times BC$
Area($\triangle ABC$) = $\frac{1}{2} \times 3 \times 4 = 6$ cm².
Also, Area($\triangle ABC$) = $\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times AC \times BD$
$6 = \frac{1}{2} \times 5 \times r$
$12 = 5r$
$r = \frac{12}{5} = 2.4$ cm.
This is the radius of the common base of the double cone.
Step 3: Find the heights of the two cones.
The double cone consists of two cones with heights AD and CD. Let $AD = h_1$ and $CD = h_2$.
In right $\triangle ABD$:
$AB^2 = AD^2 + BD^2$
$3^2 = h_1^2 + (2.4)^2$
$9 = h_1^2 + 5.76$
$h_1^2 = 9 - 5.76 = 3.24$
$h_1 = \sqrt{3.24} = 1.8$ cm.
In right $\triangle BCD$:
$BC^2 = CD^2 + BD^2$
$4^2 = h_2^2 + (2.4)^2$
$16 = h_2^2 + 5.76$
$h_2^2 = 16 - 5.76 = 10.24$
$h_2 = \sqrt{10.24} = 3.2$ cm.
(Check: $h_1 + h_2 = 1.8 + 3.2 = 5$ cm = AC)
Step 4: Calculate the volume of the double cone.
Volume = Volume of cone 1 + Volume of cone 2
$V = \frac{1}{3}\pi r^2 h_1 + \frac{1}{3}\pi r^2 h_2 = \frac{1}{3}\pi r^2 (h_1 + h_2)$
$V = \frac{1}{3}\pi r^2 (AC)$
$V = \frac{1}{3}\pi (2.4)^2 (5)$
$V = \frac{1}{3}\pi (5.76) (5)$
$V = \frac{28.8}{3}\pi = 9.6\pi$ cm³.
Using $\pi = 3.14$ (as the dimensions involve decimals):
$V = 9.6 \times 3.14 = 30.144$ cm³.
Step 5: Calculate the surface area of the double cone.
The surface area is the sum of the curved surface areas (CSA) of the two cones.
Slant height of cone 1 ($l_1$) = AB = 3 cm.
Slant height of cone 2 ($l_2$) = BC = 4 cm.
Surface Area = $\text{CSA}_1 + \text{CSA}_2 = \pi r l_1 + \pi r l_2$
Surface Area = $\pi r (l_1 + l_2)$
Surface Area = $\pi (2.4) (3 + 4)$
Surface Area = $\pi (2.4) (7) = 16.8\pi$ cm².
Using $\pi = 3.14$:
Surface Area = $16.8 \times 3.14 = 52.752$ cm².
Therefore:
The volume of the double cone is $9.6\pi$ cm³ (approximately 30.144 cm³).
The surface area of the double cone is $16.8\pi$ cm² (approximately 52.752 cm²).
Question 3. A cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?
Answer:
Given:
Internal dimensions of the cistern = 150 cm × 120 cm × 110 cm.
Initial volume of water in the cistern = 129600 cm³.
Dimensions of each brick = 22.5 cm × 7.5 cm × 6.5 cm.
Each brick absorbs $\frac{1}{17}$ of its own volume of water.
The cistern is filled with bricks until it is full to the brim.
To Find:
The maximum number of bricks (n) that can be put into the cistern without the water overflowing.
Solution:
First, calculate the total volume (capacity) of the cistern.
$V_{cistern} = \text{length} \times \text{width} \times \text{height}$
$V_{cistern} = 150 \times 120 \times 110$
$V_{cistern} = 18000 \times 110 = 1980000$ cm³
Next, calculate the volume of the cistern that is empty (needs to be filled).
$V_{empty} = V_{cistern} - V_{water\_initial}$
$V_{empty} = 1980000 - 129600 = 1850400$ cm³
This empty volume needs to be filled by the net volume occupied by the bricks.
Calculate the volume of a single brick.
$V_{brick} = \text{length} \times \text{width} \times \text{height}$
$V_{brick} = 22.5 \times 7.5 \times 6.5$
$V_{brick} = 168.75 \times 6.5 = 1096.875$ cm³
Alternatively, using fractions:
$V_{brick} = \frac{45}{2} \times \frac{15}{2} \times \frac{13}{2} = \frac{8775}{8}$ cm³
Calculate the volume of water absorbed by one brick.
$V_{absorbed} = \frac{1}{17} \times V_{brick}$
$V_{absorbed} = \frac{1}{17} \times \frac{8775}{8} = \frac{8775}{136}$ cm³
When a brick is placed in the water, it occupies its own volume ($V_{brick}$), but it also absorbs some water ($V_{absorbed}$) from the cistern. Therefore, the net increase in the occupied volume (brick + water) due to one brick is its physical volume minus the volume of water it absorbs.
Net volume increase per brick = $V_{brick} - V_{absorbed}$
Net volume increase per brick = $V_{brick} - \frac{1}{17} V_{brick}$
Net volume increase per brick = $(1 - \frac{1}{17}) V_{brick} = \frac{16}{17} V_{brick}$
Net volume increase per brick = $\frac{16}{17} \times \frac{8775}{8}$
Net volume increase per brick = $\frac{\cancel{16}^{2}}{17} \times \frac{8775}{\cancel{8}_{1}} = \frac{2 \times 8775}{17} = \frac{17550}{17}$ cm³
Let 'n' be the number of bricks that can be placed in the cistern without overflowing.
The total net volume occupied by 'n' bricks must be less than or equal to the empty volume of the cistern.
$n \times (\text{Net volume increase per brick}) \le V_{empty}$
$n \times \frac{17550}{17} \le 1850400$
Solve for n:
$n \le 1850400 \div \frac{17550}{17}$
$n \le 1850400 \times \frac{17}{17550}$
$n \le \frac{185040 \times 17}{1755}$
Perform the calculation:
$n \le \frac{3145680}{1755}$
$n \le 1792.4102...$
Since the number of bricks must be a whole number, the maximum number of bricks that can be put in without overflowing is the largest integer less than or equal to 1792.41...
$n = 1792$
Therefore, 1792 bricks can be put into the cistern without the water overflowing.
Question 4. In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 7280 km2 , show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.
Answer:
Given:
Rainfall depth in the river valley $= 10 \text{ cm}$
Area of the river valley $= 7280 \text{ km}^2$
Dimensions of each of the three rivers:
Length $= 1072 \text{ km}$
Width $= 75 \text{ m}$
Depth $= 3 \text{ m}$
To Show:
The total rainfall volume is approximately equivalent to the volume of water in three rivers.
Solution:
First, we calculate the volume of rainfall in the valley.
We need to express all dimensions in the same unit, preferably kilometers.
Rainfall depth $= 10 \text{ cm}$
Since $1 \text{ m} = 100 \text{ cm}$ and $1 \text{ km} = 1000 \text{ m}$, we have:
$1 \text{ cm} = \frac{1}{100} \text{ m} = \frac{1}{100 \times 1000} \text{ km} = \frac{1}{100000} \text{ km} = 10^{-5} \text{ km}$
Rainfall depth $= 10 \text{ cm} = 10 \times 10^{-5} \text{ km} = 10^{-4} \text{ km} = 0.0001 \text{ km}$
Area of the valley $= 7280 \text{ km}^2$
Volume of rainfall $=$ Area of valley $\times$ Rainfall depth
$V_{\text{rainfall}} = 7280 \text{ km}^2 \times 0.0001 \text{ km}$
$V_{\text{rainfall}} = 0.7280 \text{ km}^3$
Next, we calculate the volume of water in one river and then in three rivers.
We convert the width and depth of the river from meters to kilometers.
$1 \text{ m} = 10^{-3} \text{ km} = 0.001 \text{ km}$
River Length $= 1072 \text{ km}$
River Width $= 75 \text{ m} = 75 \times 10^{-3} \text{ km} = 0.075 \text{ km}$
River Depth $= 3 \text{ m} = 3 \times 10^{-3} \text{ km} = 0.003 \text{ km}$
Volume of one river $=$ Length $\times$ Width $\times$ Depth
$V_{\text{one river}} = 1072 \text{ km} \times 0.075 \text{ km} \times 0.003 \text{ km}$
$V_{\text{one river}} = 1072 \times (0.075 \times 0.003) \text{ km}^3$
$V_{\text{one river}} = 1072 \times 0.000225 \text{ km}^3$
$V_{\text{one river}} = 0.2412 \text{ km}^3$
Total volume of water in three rivers $= 3 \times V_{\text{one river}}$
$V_{\text{three rivers}} = 3 \times 0.2412 \text{ km}^3$
$V_{\text{three rivers}} = 0.7236 \text{ km}^3$
Now we compare the total rainfall volume and the total volume of water in three rivers.
Rainfall volume $= 0.7280 \text{ km}^3$
Volume of three rivers $= 0.7236 \text{ km}^3$
The two calculated volumes are very close to each other ($0.7280 \text{ km}^3$ and $0.7236 \text{ km}^3$).
The difference between the volumes is $|0.7280 - 0.7236| \text{ km}^3 = 0.0044 \text{ km}^3$, which is a small difference relative to the total volumes.
Hence, the total rainfall of 10 cm in the valley was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.
Thus, the statement is shown to be true.
Question 5. An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see Fig. 13.25).

Answer:
Given:
Height of the cylindrical portion ($h_c$) = $10 \text{ cm}$
Total height of the funnel ($H$) = $22 \text{ cm}$
Diameter of the cylindrical portion ($d_c$) = $8 \text{ cm}$
Diameter of the top of the funnel ($d_f$) = $18 \text{ cm}$
To Find:
The area of the tin sheet required to make the funnel.
Solution:
The funnel is made up of a cylindrical portion and a frustum of a cone.
The area of the tin sheet required is the sum of the curved surface area of the cylindrical portion and the curved surface area of the frustum of the cone.
First, calculate the dimensions of the cylindrical part:
Radius of the cylindrical base ($r_c$) = $\frac{d_c}{2} = \frac{8}{2} = 4 \text{ cm}$
Height of the cylindrical portion ($h_c$) = $10 \text{ cm}$
Curved surface area of the cylindrical portion:
$CSA_{\text{cylinder}} = 2 \pi r_c h_c$
$CSA_{\text{cylinder}} = 2 \times \pi \times 4 \times 10$
$CSA_{\text{cylinder}} = 80 \pi \text{ cm}^2$
Next, calculate the dimensions of the frustum part:
Height of the frustum ($h_f$) = Total height - Height of cylindrical portion
$h_f = H - h_c = 22 - 10 = 12 \text{ cm}$
Radius of the base of the frustum ($r_1$) = Radius of the top of the cylinder = $r_c = 4 \text{ cm}$
Radius of the top of the frustum ($r_2$) = $\frac{d_f}{2} = \frac{18}{2} = 9 \text{ cm}$
Slant height of the frustum ($l$):
$l = \sqrt{h_f^2 + (r_2 - r_1)^2}$
$l = \sqrt{12^2 + (9 - 4)^2}$
$l = \sqrt{12^2 + 5^2}$
$l = \sqrt{144 + 25}$
$l = \sqrt{169}$
$l = 13 \text{ cm}$
Curved surface area of the frustum of the cone:
$CSA_{\text{frustum}} = \pi (r_1 + r_2) l$
$CSA_{\text{frustum}} = \pi (4 + 9) \times 13$
$CSA_{\text{frustum}} = \pi (13) \times 13$
$CSA_{\text{frustum}} = 169 \pi \text{ cm}^2$
Total area of the tin sheet required:
Total Area = $CSA_{\text{cylinder}} + CSA_{\text{frustum}}$
Total Area = $80 \pi + 169 \pi$
Total Area = $(80 + 169) \pi$
Total Area = $249 \pi \text{ cm}^2$
Using $\pi = \frac{22}{7}$:
Total Area = $249 \times \frac{22}{7}$
Total Area = $\frac{5478}{7} \text{ cm}^2$
Total Area $\approx 782.57 \text{ cm}^2$
The area of the tin sheet required to make the funnel is $\frac{5478}{7} \text{ cm}^2$ or approximately $782.57 \text{ cm}^2$.
Question 6. Derive the formula for the curved surface area and total surface area of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.
Answer:
Given:
A frustum of a cone obtained by cutting a right circular cone by a plane parallel to its base.
Let $r_1$ be the radius of the larger circular base.
Let $r_2$ be the radius of the smaller circular base ($r_1 > r_2$).
Let $h$ be the height of the frustum.
Let $l$ be the slant height of the frustum.
Let the original cone (from which the frustum is cut) have height $H$ and slant height $L$. The radius of the base of the original cone is $r_1$.
The small cone that is removed from the top has height $(H-h)$, slant height $(L-l)$, and radius $r_2$.
To Derive:
1. Formula for the curved surface area ($CSA$) of the frustum.
2. Formula for the total surface area ($TSA$) of the frustum.
Derivation:
Consider the cross-section of the cone and the frustum formed by a plane passing through the axis. This cross-section is a trapezium, formed from a large triangle (representing the original cone) minus a small triangle (representing the cone removed from the top).
The triangles formed by the axis, height, and radius (or slant height) are similar. Let the vertex of the original cone be $V$. Let the centres of the larger and smaller bases of the frustum be $O_1$ and $O_2$ respectively. Let $A$ and $B$ be points on the circumference of the larger base, and $C$ and $D$ be points on the circumference of the smaller base, such that $O_1A = r_1$, $O_2C = r_2$. The height of the frustum is $O_1O_2 = h$, and the slant height is $AC = l$. The height of the original cone is $VO_1 = H$ and slant height $VA = L$. The height of the removed cone is $VO_2 = H-h$ and slant height $VC = L-l$.
From similar triangles $VO_2C$ and $VO_1A$ (or similar triangles formed by slant heights $VCA$ and $VOA$):
$\frac{VO_2}{VO_1} = \frac{O_2C}{O_1A} = \frac{VC}{VA}$
$\frac{H-h}{H} = \frac{r_2}{r_1} = \frac{L-l}{L}$
1. Formula for the slant height of the frustum ($l$):
Consider the right-angled triangle formed by dropping a perpendicular from a point on the circumference of the smaller base to the plane of the larger base. Let this point be $C$ on the smaller base (radius $r_2$) and drop a perpendicular $CE$ to the plane of the larger base. Then $O_2O_1CE$ forms a rectangle, so $O_2O_1 = CE = h$ and $O_2E = O_1C$. Point $E$ will lie on the radius $O_1A$. Then $EA = O_1A - O_1E = O_1A - O_2C = r_1 - r_2$. The slant height $AC = l$ is the hypotenuse of the right-angled triangle $CEA$.
By Pythagoras theorem in $\triangle CEA$:
$AC^2 = CE^2 + EA^2$
$l^2 = h^2 + (r_1 - r_2)^2$
$l = \sqrt{h^2 + (r_1 - r_2)^2}$
2. Formula for the Curved Surface Area (CSA) of the frustum:
The curved surface area of the frustum is the curved surface area of the original cone minus the curved surface area of the small cone that is removed.
$CSA_{\text{frustum}} = CSA_{\text{original cone}} - CSA_{\text{removed cone}}$
$CSA_{\text{frustum}} = \pi r_1 L - \pi r_2 (L-l)$
$CSA_{\text{frustum}} = \pi [r_1 L - r_2 (L-l)]$
From the similar triangles relation, we have $\frac{L-l}{L} = \frac{r_2}{r_1}$.
This gives $r_1 (L-l) = r_2 L$, or $r_1 L - r_1 l = r_2 L$.
Rearranging this equation to express $L$: $r_1 L - r_2 L = r_1 l \implies L(r_1 - r_2) = r_1 l \implies L = \frac{r_1 l}{r_1 - r_2}$.
Substitute the expression for $L$ into the CSA formula:
$CSA_{\text{frustum}} = \pi \left[ r_1 \left(\frac{r_1 l}{r_1 - r_2}\right) - r_2 \left(\frac{r_1 l}{r_1 - r_2} - l\right) \right]$
$CSA_{\text{frustum}} = \pi \left[ \frac{r_1^2 l}{r_1 - r_2} - r_2 \left(\frac{r_1 l - l(r_1 - r_2)}{r_1 - r_2}\right) \right]$
$CSA_{\text{frustum}} = \pi \left[ \frac{r_1^2 l}{r_1 - r_2} - r_2 \left(\frac{r_1 l - r_1 l + r_2 l}{r_1 - r_2}\right) \right]$
$CSA_{\text{frustum}} = \pi \left[ \frac{r_1^2 l}{r_1 - r_2} - \frac{r_2 (r_2 l)}{r_1 - r_2} \right]$
$CSA_{\text{frustum}} = \pi \frac{l (r_1^2 - r_2^2)}{r_1 - r_2}$
Using the difference of squares identity, $r_1^2 - r_2^2 = (r_1 - r_2)(r_1 + r_2)$:
$CSA_{\text{frustum}} = \pi \frac{l (r_1 - r_2)(r_1 + r_2)}{r_1 - r_2}$
Assuming $r_1 \neq r_2$, we can cancel $(r_1 - r_2)$ from the numerator and denominator:
$CSA_{\text{frustum}} = \pi l (r_1 + r_2)$
So, the curved surface area of a frustum of a cone is given by $CSA = \pi (r_1 + r_2) l$, where $l = \sqrt{h^2 + (r_1 - r_2)^2}$.
3. Formula for the Total Surface Area (TSA) of the frustum:
The total surface area of the frustum is the sum of the curved surface area and the areas of the two circular bases.
Area of the larger base $= \pi r_1^2$
Area of the smaller base $= \pi r_2^2$
$TSA_{\text{frustum}} = CSA_{\text{frustum}} + \text{Area of larger base} + \text{Area of smaller base}$
$TSA_{\text{frustum}} = \pi (r_1 + r_2) l + \pi r_1^2 + \pi r_2^2$
So, the total surface area of a frustum of a cone is given by $TSA = \pi l (r_1 + r_2) + \pi r_1^2 + \pi r_2^2$, where $l = \sqrt{h^2 + (r_1 - r_2)^2}$.
Question 7. Derive the formula for the volume of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.
Answer:
Given:
A frustum of a cone formed by cutting a right circular cone by a plane parallel to its base.
Let $r_1$ be the radius of the larger circular base.
Let $r_2$ be the radius of the smaller circular base ($r_1 > r_2$).
Let $h$ be the height of the frustum.
Let the original cone from which the frustum is obtained have height $H$ and radius of base $r_1$.
Let the small cone that is removed from the top have height $H'$ and radius of base $r_2$.
From the geometry, the height of the removed cone is $H' = H - h$.
To Derive:
The formula for the volume ($V$) of the frustum of the cone.
Derivation:
The volume of the frustum of a cone is the difference between the volume of the original cone and the volume of the small cone that is removed from the top.
$V_{\text{frustum}} = V_{\text{original cone}} - V_{\text{removed cone}}$
The volume of a cone with radius $r$ and height $h$ is given by $\frac{1}{3} \pi r^2 h$.
So, $V_{\text{original cone}} = \frac{1}{3} \pi r_1^2 H$
And $V_{\text{removed cone}} = \frac{1}{3} \pi r_2^2 H'$
Thus, $V_{\text{frustum}} = \frac{1}{3} \pi r_1^2 H - \frac{1}{3} \pi r_2^2 H'$
Consider the vertical cross-section of the original cone and the removed cone passing through the axis. This forms two similar triangles.
From the similarity of the triangles formed by the heights and radii, we have:
$\frac{H'}{H} = \frac{r_2}{r_1}$
... (i)
Also, $H' = H - h$. Substituting this into equation (i):
$\frac{H-h}{H} = \frac{r_2}{r_1}$
... (ii)
From equation (ii), we can express $H$ in terms of $h, r_1,$ and $r_2$:
$r_1(H - h) = r_2 H$
$r_1 H - r_1 h = r_2 H$
$r_1 H - r_2 H = r_1 h$
$H (r_1 - r_2) = r_1 h$
$H = \frac{r_1 h}{r_1 - r_2}$
Now, we find $H'$ using $H' = H - h$:
$H' = \frac{r_1 h}{r_1 - r_2} - h$
$H' = \frac{r_1 h - h(r_1 - r_2)}{r_1 - r_2}$
$H' = \frac{r_1 h - r_1 h + r_2 h}{r_1 - r_2}$
$H' = \frac{r_2 h}{r_1 - r_2}$
Now substitute the expressions for $H$ and $H'$ into the volume formula for the frustum:
$V_{\text{frustum}} = \frac{1}{3} \pi r_1^2 \left(\frac{r_1 h}{r_1 - r_2}\right) - \frac{1}{3} \pi r_2^2 \left(\frac{r_2 h}{r_1 - r_2}\right)$
$V_{\text{frustum}} = \frac{1}{3} \pi h \left( \frac{r_1^3}{r_1 - r_2} - \frac{r_2^3}{r_1 - r_2} \right)$
$V_{\text{frustum}} = \frac{1}{3} \pi h \left( \frac{r_1^3 - r_2^3}{r_1 - r_2} \right)$
Using the algebraic identity $a^3 - b^3 = (a - b)(a^2 + ab + b^2)$, we have $r_1^3 - r_2^3 = (r_1 - r_2)(r_1^2 + r_1 r_2 + r_2^2)$.
Substitute this into the expression for $V_{\text{frustum}}$:
$V_{\text{frustum}} = \frac{1}{3} \pi h \left( \frac{(r_1 - r_2)(r_1^2 + r_1 r_2 + r_2^2)}{r_1 - r_2} \right)$
Assuming $r_1 \neq r_2$, we can cancel $(r_1 - r_2)$ from the numerator and denominator.
$V_{\text{frustum}} = \frac{1}{3} \pi h (r_1^2 + r_1 r_2 + r_2^2)$
Thus, the volume of the frustum of a cone is given by $V = \frac{1}{3} \pi h (r_1^2 + r_2^2 + r_1 r_2)$.

